Feladat: F.1928 Korcsoport: 18- Nehézségi fok: -
Füzet: 1976/november, 113 - 115. oldal  PDF  |  MathML 
Témakör(ök): Beírt alakzatok, Szélsőérték differenciálszámítással, Kocka, Egyenes körkúpok, Térfogat, Feladat
Hivatkozás(ok):Feladatok: 1974/március: F.1928

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a kocka tengelyül kiszemelt testátlójának végpontjait A-val és B-vel, centrumát C-vel, az A-val szomszédos csúcsait A1-gyel, A2-vel, A3-mal, Ai-nek C-re vonatkozó tükörképét Bi-vel (i=1,2,3). Határozzuk meg először a kocka azon pontjainak a mértani helyét, amelyeket az AB tengely körül tetszőleges szöggel elforgatva ismét a kockához tartozó pontot kapunk. Jelöljük e mértani helyet M-mel, a kockából kivágható, AB tengely körül tetszőleges forgáskúp nyilván M-nek is része.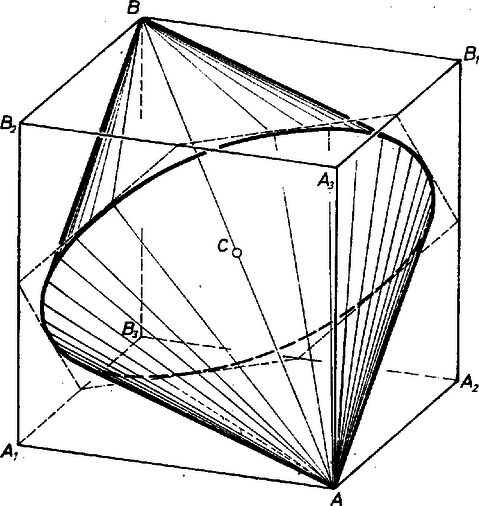

 

 

1. ábra
 

Vizsgáljuk először M-nek az AB1BA1 síkkal alkotott M0 metszetét. Ez nyilván része az AB1BA1 téglalap AB körüli 180∘-os forgatásából származó AB1*BA1* téglalapnak is, megmutatjuk, hogy az M0 metszet e két téglalap közös része.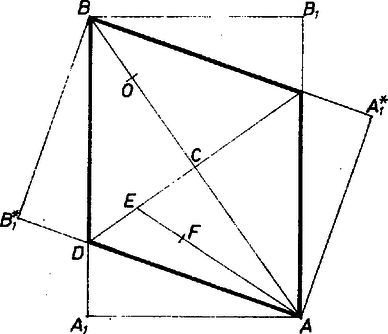
 

 

2. ábra
 

Ebből már következik, hogy M-et úgy kapjuk meg, hogy e közös részt AB körül megforgatjuk.
Jelöljük AB1* és A1B metszéspontját D-vel. Elég megmutatnunk, hogy D benne van M0-ban, hiszen, ha ezt már beláttuk, akkor az, hogy a CD szakasz tetszőleges E pontja és hogy az AE szakasz tetszőleges F pontja M0-hoz tartozik, következik abból, hogy M0 konvex, a metszet többi pontja pedig megkapható az ACD háromszög pontjaiból AB-re, illetve C-re való tükrözéssel (M0 is és M is nyilvánvalóan szimmetrikus az AB tengelyre és a C centrumra nézve). Az pedig, hogy M0 konvex, következik abból, hogy konvex alakzatok közös része is konvex, és M0 a konvex kocka AB körüli forgatásából származó konvex kockák közös részeként keletkező M testnek, és az ugyancsak konvex AB1BA1 síknak a metszete. Valóban, ha adott konvex alakzatok tetszőleges serege a térben és a P,Q pontok ezeknek az alakzatoknak mindegyikében benne vannak, akkor a PQ szakasz tetszőleges pontja is benne van az alakzatok közül mindegyikben (hiszen az alakzatok konvexek), tehát a PQ szakasz minden pontja benne van az alakzatok közös részében is.
Lássuk tehát, miért is van benne D az M-ben. D minden esetre benne van az AB szakasz S felező merőleges síkjában, tehát azonos az S sík és a kocka metszetének az A1B egyenesen levő pontjával. Ismeretes, hogy ez a metszet szabályos hatszög, amelynek a csúcsai az A1B2,B2A3,A3B1,B1A2,A2B3,B3A1 szakaszok felezőpontjai és D e hatszög egyik oldalának a felezőpontja. Tehát D-t AB körül forgatva a hatszögbe írt kört kapjuk, amelynek minden pontja benne van a hatszögben, így a kockában is. Eredeti célunkra rátérve vizsgáljuk meg most már, mekkora az ABD háromszög AB körüli forgatásából származó M kettős kúpba írható maximális térfogatú kúp. A keresett kúp alapkörének a középpontja rajta van az AB szakaszon, jelöljük O-val. Az általánosság megszorítása nélkül azt is feltehetjük, hogy O az AB szakasz BC felén van. Rögzített O mellett a kúp alapköre már meg van határozva, a közös O-hoz tartozó kúpok közül tehát annak a térfogata a maximális, amelyiknek a magassága maximális, vagyis amelyiknek a csúcsa O-tól legtávolabb van. Mivel e csúcs is rajta van AB-n, csak A lehet (ha O azonos C-vel, B is lehetne, de ez nem jelent lényegesen új lehetőséget). Jelöljük a kocka élét a-val, a kúp magasságát m-mel, alapkörének a sugarát r-rel. Ekkor AB=a3 és hasonló háromszögek alapján kapjuk, hogy
r:(a3-m)=AA1:A1B,r=a3-m2,
tehát a kúp térfogata
V=mr2π3=π6m(a3-m)2,
ahol a32≤m<a3. Most már V-nek m szerinti deriváltja,
dVdm=π6[(=a3-m)2-2m(a3-m)]=π6(a3-m)(a3-2m)
a mondott szakaszon negatív, V tehát m növelésével monoton fogy, így V akkor maximális, ha m minimális, azaz m=a32, vagyis O azonos C-vel. Ekkor r=a322, és V=π6m3=π316a3=0,34a3, ami elég nagy pazarlásnak látszik, de ha arra gondolunk, hogy ilyen kúpot mindjárt kettőt is kivághatunk a kockából, e pazarlás érthetővé válik.