Kezdőlap


Feladat:	F.1922	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1975/január, 6 - 8. oldal		PDF \| MathML
Témakör(ök):	Hossz, kerület, Diszkusszió, Négyszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1974/február: F.1922

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Keressük a kívánt alakzatnak egy olyan módosítását, amelyben kihasználhatjuk az átlók egyenlőségét és merőleges helyzetét. Toljuk el evégett az egyik átlót úgy, hogy valamelyik végpontja essék egybe a másik átló valamelyik végpontjával. Célszerű egybeeső végpontnak $B$ -t vagy $C$ -t választani, mert ezekből a kívánt négyszögnek $2 - 2$ ismert hosszúságú oldala indul ki, míg $A$ -ból, $D$ -ből cs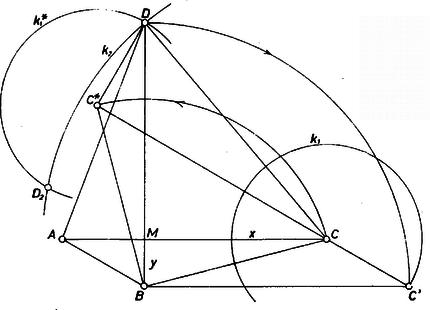ak $1 - 1$ .
Toljuk el hát az $A C$ átlót az $\vec{A B}$ -ral a $B C'$ helyzetbe (1. ábra).

1. ábra

Így a

D

pont előáll

C'

-ből

B

mint centrum körüli

90^{\circ}

-os elfordítással, másrészt ismerjük mindkét pontnak, és a

B

-nek is, a

C

-től való távolságát. Eszerint

C

-t és

B

-t egymástól az adott távolságban lerögzítve, a

C'

és

D

pontok számára két-két mértani helyet rajzolhatunk meg: a

C

körüli

A B

, illetve

C D

sugarú

k_{1}

, ill.

k_{2}

kört, valamint ezeknek

B

körüli,

90^{\circ}

-kal való elfordítottját,

k_{2}^{*}

-ot,

k_{1}^{*}

-ot, természetesen egymással ellentétes irányú elfordítással. (Az ábrán

k_{1}^{*}

közepe

C^{*}

k_{2}^{*}

-ot mellőzhetjük.) Ekkor

D

k_{2}

és

k_{2}^{*}

valamelyik közös pontja, ebből

C'

-t

90^{\circ}

-os visszafordítással kapjuk

k_{1}

-en, végül

A

-t a

B

-ből a

\vec{C' C}

-ral való visszatolással.
Az előírt méretek mellett

k_{2}

és

k_{1}^{*}

két pontban metszi egymást, az egyik metszéspontból a négyszög konvexnek adódik (1. ábra), ez tehát megfelel; a másikból (2. ábra,

C^{*}

D_{2}

és

A_{2}

) hurkoltnak, ez nem felel meg.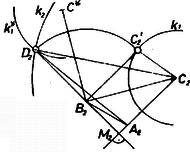

2. ábra

b) Az átlók hosszát csak az 1. ábra esetében számítjuk, a végzett szerkesztés alapján. A

B D C^{*}

háromszögben

C^{*} D = 2

C^{*} B = 4

és a köztük levő szög

C C^{*} B ∢ = 45^{\circ}

-kal nagyobb, mint a

C D C^{*}

háromszög

C^{*}

-nál levő szöge. Az utóbbi háromszögben

C C^{*} = 4 \sqrt[]{2}

, így

\begin{matrix} cos C C^{*} D ∢ = \frac{{(4 \sqrt[]{2})}^{2} + 2^{2} - 6^{2}}{2 \cdot 4 \sqrt[]{2} \cdot 2} = 0, \end{matrix}

a szög

90^{\circ}

, ennélfogva

B D^{2} = B C^{* 2} + C^{*} D^{2} - 2 B C^{*} \cdot C^{*} D cos 135^{\circ} = 20 + 8 \sqrt[]{2}

\begin{matrix} B D = 5, 596 egység . \end{matrix}

II. megoldás a feladat a) részéhez. Legyen az

A B

B C

C D

oldal felezőpontja rendre

P

Q

R

, ezekre a föltevésekből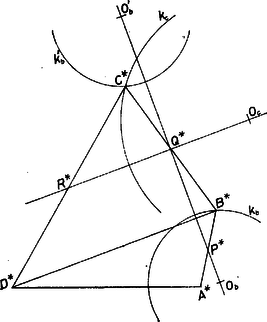

\begin{matrix} P Q = \frac{1}{2} A C = \frac{1}{2} B D = Q R és P Q R ∢ = 90^{\circ}, \end{matrix}

mert

P Q | | A C ⊥ B D | | Q R

. Ezek alapján egy tetszőleges

P^{*} Q^{*} R^{*}

egyenlő szárú derékszögű háromszögből kiindulva a keresetthez hasonló négyszöget szerkesztünk. Felhasználjuk, hogy ábránk bármely nagyított képén

B^{*} P^{*} : B^{*} Q^{*} = = 1 : 2

C^{*} Q^{*} : C^{*} R^{*} = 2 : 3

, tehát

B^{*}

P^{*}

Q^{*}

alappontpár

1 : 2

arányú

k_{b}

Apollóniosz-körén van,

C^{*}

Q^{*}

R^{*}

pár

2 : 3

arányú

k_{c}

, Apollóniosz-körén, és hogy

C^{*}

B^{*}

-nak tükörképe

Q^{*}

-ra, tehát

C^{*}

k_{b}

-nek

Q^{*}

-ra való

k'_{b}

tükörképén is rajta van (3. ábra).

3. ábra

Így

k_{c}

, és

k'_{b}

, közös pontja

C^{*}

, ennek tükörképe

R^{*}

-ra

D^{*}

, a

Q^{*}

-ra

B^{*}

, végül

B^{*}

képe

P^{*}

-ra

A^{*}

. Végül az

A^{*} B^{*} C^{*} D^{*}

négyszöget kellően nagyítjuk vagy kicsinyítjük.
Az átlók kiszámítása ennek a szerkesztésnek az alapján is elvégezhető, pl. abban a koordináta-rendszerben, melynek origója

Q^{*}

, és tengelyei átmennek

P^{*}

-on, ill.

R^{*}

-on.

III. megoldás a feladat b) részéhez. Legyen az átlók hossza

d

, metszéspontjuk

M

és egyik-egyik részük

M C = x

M B = y

, ahol a konvexség miatt

0 < x < d

és

0 < y < d

. Ezekre

\begin{matrix} {(d - x)}^{2} + y^{2} = & 4, & (1) \\ x^{2} + y^{2} = & 16, & (2) \\ x^{2} + {(d - y)}^{2} = & 36. & (3) \end{matrix}

Levonva (2)-t (1)-ből és (3)-ból,

x

-re,

y

-ra elsőfokú egyenlet adódik, és abból

\begin{matrix} x = \frac{d^{2} + 12}{2 d}, y = \frac{d^{2} - 20}{2 d} . \end{matrix}

(4)

Ezeket (2)-be beírva

d^{2}

-re kapunk másodfokú egyenletet:

\begin{matrix} d^{4} - 40 d^{2} + 272 = 0, d^{2} = 20 \pm 8 \sqrt[]{2}, \end{matrix}

de a kisebbik gyök (4) szerint negatív

y

-t adna, azt nem használhatjuk.

d^{2}

nagyobbik értéke egyezik az I. megoldásbelivel.