Feladat:	F.1915	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Dozmati Zoltán
Füzet:	1975/március, 109 - 112. oldal		PDF  |  MathML
Témakör(ök):	Párhuzamos szelők tétele, Síkgeometriai számítások trigonometria nélkül sokszögekben, Síkgeometriai szerkesztések, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1974/január: F.1915

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 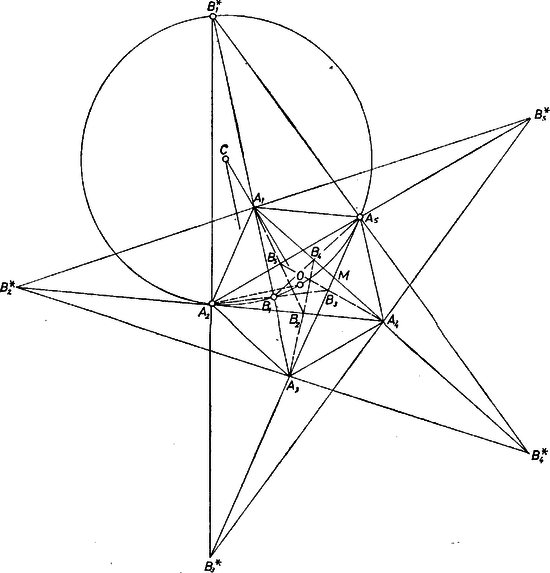$\begin{array}{c}{\displaystyle \frac{A_1{B}_1}{B_1{A}_3}\text{és}\frac{A_3{B}_3}{B_3{A}_5}}\end{array}$ (1) I. megoldás. 1. Szerkesztés útján határozzuk meg az $A_1{A}_3$ átlószakasz kívánt tulajdonságú $B_1$ pontját (1. ábra).     1. ábra   Erre $A_1{B}_1$ és $B_1{A}_3$ egyirányú szakaszok, arányuk pozitív, ezért egyirányúak az $A_3{B}_3$ és $B_3{A}_5$ szakaszok is, tehát $B_3$ az $A_3{A}_5$ átlószakasz belső pontja. (Ha ugyanis $B_3$ az $A_3{A}_5$-nek akármelyik meghosszabbításán keletkeznék, akkor belőle csak megfordulással juthatnánk $A_5$-be, és így az (1)-beli második hányados negatív lenne, a követelménnyel ellentétben.) Másrészt $A_1{A}_3=A_3{A}_5$ alapján $A_1{B}_1=A_3{B}_3$, továbbá $B_1{A}_3=B_3{A}_5$. Ugyanis $B_1$-gyel $A_1$-től $A_3$ felé haladva, az arány szigorúan monoton nő, azaz minden pozitív értéket csak egyszer vesz fel. Valóban ha $X$, $Y$ az $A_1{A}_3$ szakasz pontjai úgy, hogy $A_{1}Y>A_{1}X$ ‐ tehát egyszersmind $Y{A}_3<X{A}_3$ ‐, akkor $\begin{array}{c}{\displaystyle \frac{A_{1}Y}{Y{A}_3}=\frac{A_{1}X+XY}{Y{A}_3}>\frac{A_{1}X}{Y{A}_3}>\frac{A_{1}X}{X{A}_3}\mathrm{.}}\end{array}$ Mivel az ötszög szabályos, azért az $O$ középpontja körüli $\left(2/5\right)\cdot {360}^{\circ }={144}^{\circ }$-os elfordítással $A_1$ az $A_3$-ba jut, egyidejűen $A_3$ az $A_5$-be, és az előbbiek alapján $B_1$ a $B_3$-ba. Eszerint $O{B}_1{B}_3$ egyenlő szárú háromszög, és a $B_1{B}_3$ alapon levő szögei ${18}^{\circ }$-osak. Az $A_2$ csúcs az alap $B_1$-en túli meghosszabbításán van, hiszen az $A_1{A}_3$ egyenes elválasztja $A_2$-t az $A_3{A}_5$ szakasztól; így $O{B}_1{A}_2\sphericalangle ={180}^{\circ }-{18}^{\circ }={162}^{\circ }$. Belátjuk még, hogy nem lehet $B_1$ az $O{A}_2$ egyenesnek azon az oldalán, amelyiken $A_1$ van, más szóval, hogy $A_1{B}_1:B_1{A}_3>1$ (hiszen $O{A}_2$ az $A_1{A}_3$ átlószakasz felező merőlegese). Ugyanis az $O{A}_2$ egyenes átmegy az $A_1{A}_3{A}_4{A}_5$ szimmetrikus trapéz átlóinak $M$ metszéspontján, és az $A_1{B}_1:B_1{A}_3<1$, azaz $A_1{B}_1<B_1{A}_3$ nagyságviszony mellett $B_3$ az $M{A}_5$ szakaszon keletkeznék, akkor pedig $A_3{B}_3>A_{3}M>M{A}_5>B_3{A}_5$ lenne, és $A_3{B}_3:B_3{A}_5=A_1{B}_1:B_1{A}_3>1$. (Az $A_{3}M>M{A}_5$ nagyságviszony az $A_1{A}_3>A_4{A}_5$-ből következik.) Eszerint $B_1$ az $O{A}_2$ szakasznak azon a ${162}^{\circ }$-os (vagyis tompaszögű) látókörívén van rajta, melynek $C$ középpontja az $O{A}_2$ egyenesnek $A_1$-et tartalmazó oldalán van, és $OC{A}_2\sphericalangle ={360}^{\circ }-2\cdot {162}^{\circ }={36}^{\circ }$. Könnyen látható, hogy ekkor $A_{2}OC\sphericalangle ={72}^{\circ }$, tehát $C$-t az $O{A}_2$ szakasz felező merőlegeséből az $O{A}_1$ egyenes metszi ki.   2. Hasonlóan kapunk megfelelő $B_1^{*}$ pontot $A_1{A}_3$-nak $A_1$-en túli meghosszabbításán. Ennek a meghosszabbításnak bármely pontját $A_2$-vel összekötve, az egyenes az $A_3{A}_5$ egyenest az $A_3$-on túli meghosszabbításon metszi (hiszen egyenesünk nem lépheti át az $A_2$-n át $A_3{A}_5$-tel párhuzamosan húzott egyenest, ami az $A_2{A}_1$). Így az (1)-beli hányadosok mindegyike negatív és $B_1^{*}$-ra, valamint a hozzá tartozó $B_3^{*}$-ra $A_1{B}_1^{*}=A_3{B}_3^{*}$; ezt a fentiekhez hasonlóan láthatjuk be. Ezek szerint $B_1^{*}$ és $B_3^{*}$ is egymásba mennek át a fenti ${144}^{\circ }$-os elfordítással. De mivel itt $O{A}_2$ elválasztja $B_1^{*}$-ot és $B_3^{*}$-ot, azért $A_2{B}_1^{*}O\sphericalangle ={18}^{\circ }$, tehát $B_1^{*}$ a fenti látókörív kiegészítő ívén van, egy csapásra kimetszhető $A_1{A}_3$-ból mint a $C$ körüli $CO$ sugarú kör másik metszéspontja.   3. $A_1{A}_3$-nak $A_3$-on túli meghosszabbításán nem található megfelelő $B_1$. Erre ugyanis abszolút értékben $A_1{B}_1>A_3{B}_1$ lenne, másrészt $B_3$ az $A_3{A}_5$-nek $A_3$-on túli meghosszabbításán keletkezne, így $A_3{B}_3<A_5{B}_3$, tehát az (1)-beli arányok nem lehetnek egyenlők (csak előjelük egyező, mindkettő negatív). Ezzel a megoldást befejeztük.    Sok kiegészítéssel Dozmati Zoltán (Győr, Révai M. Gimn., III. o. t.) ötlete alapján.   Megjegyzés. Hasonlóan értelmezve $A_4{B}_3$ és $A_2{A}_5$ metszéspontjaként $B_5$-öt, és így tovább a $B_2$, $B_4$ pontot, azt mondhatjuk, hogy a $B_1{B}_3{B}_5{B}_2{B}_4$ hurkolt ötszög bele van írva az $A_1{A}_3{A}_5{A}_2{A}_4$ szabályos csillagötszögbe, és megfordítva, az $A_2{A}_4{A}_1{A}_3{A}_5$ szabályos csillagötszög bele van írva a $B_1{B}_3{B}_5{B}_2{B}_4$ hurkolt ötszögbe, vagyis e két hurkolt ötszög egymásba van beleírva. Ez a megállapítás a $B_1^{*}$-ból adódó alakzatra is érvényes. ‐ Egyébként könnyű belátni, hogy $B_1{B}_3{B}_5{B}_2{B}_4$ is szabályos csillagötszög.   II. megoldás. Számítással határozzuk meg $B_1$ helyzetét abból, hogy a $B_1$-et meghatározó $A_2{B}_3$ és $A_1{A}_3$ egyeneseket két párhuzamos egyenes metszi át: $A_1{A}_2$ és $A_3{A}_5$. Válasszuk pozitívnak az $A_1$-ből $A_3$-ba és az $A_3$ ból $A_5$-be mutató irányt, és legyen irány és nagyság szerint $A_1{B}_1=A_3{B}_3=x$, továbbá $A_1{A}_3=A_3{A}_5=d$ az ötszög átlója, végül $A_2{A}_1=a$ az oldala. A párhuzamos szelők tétele alapján $\begin{array}{c}{\displaystyle B_1{A}_1:A_1{A}_2=B_1{A}_3:A_3{B}_3}\end{array}$ (nagyság és irány szerint, felhasználva az összetartozó $B_1$ és $B_3$ lehetséges helyzeteiről az I. megoldásban látottakat), illetve rövid jelöléseinkkel ${\displaystyle \begin{array}{c}\hfill {\displaystyle -x:-a=\left(d-x\right):x\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2+ax-ad=0.}\hfill \end{array}}$ Rendezzük át ezt az egyenletet úgy, hogy a szerkesztés menete kiolvasható legyen belőle: 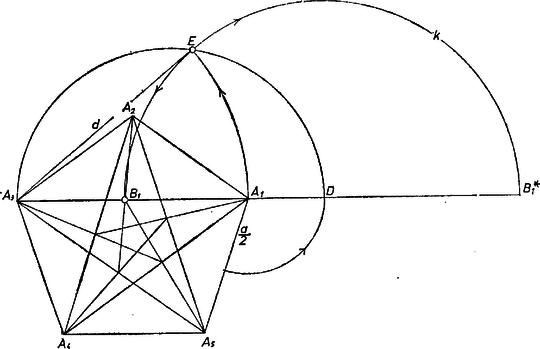$\begin{array}{c}{\displaystyle {\left(x+\frac{a}{2}\right)}^2={\left(d+\frac{a}{2}\right)}^2-d^2;}\end{array}$ Mérjük fel tehát az $A_3{A}_1$ egyenes $A_1$-en túli meghosszabbítására $A_1$-ből kiindulva az $\frac{a}{2}$ szakaszt, a végpontja legyen $D$ (2. ábra).     2. ábra   Rajzoljunk Thalész-kört $A_{3}D$ fölé, és messük el az $A_3$ körüli, $A_1$-en átmenő körrel: ez az $E$ pont. Ekkor a $DE$ szakasz hossza egyenlő $x+\frac{a}{2}$ abszolút értékével. A $D$ körüli, $E$-n átmenő $k$ körnek az $A_1{A}_3$ szakaszon levő $B_1$ metszéspontjára $x_1=A_1{B}_1=DE-a/2$, ez tehát az egyenlet gyöke. Legyen $k$-nak az $A_1{A}_3$ egyenessel alkotott második metszéspontja $B_1^{*}$, akkor $x_2=-A_1{B}_1^{*}=-DE-a/2$ az egyenlet másik gyöke. Tehát $B_1$, $B_1^{*}$ a keresett pontok.