Feladat: F.1909 Korcsoport: 16-17 Nehézségi fok: -
Megoldó(k):  Alexy M. ,  Baranyi J. ,  Bárdossy Gy. ,  Bezdek A. ,  Csuka Ibolya ,  Dózsa L. ,  Hamar D. ,  Ható Mária ,  József S. ,  Karsai B. ,  Kecskés Cs. ,  Kerner P. ,  Király Mária ,  Kiss E. ,  Kóczy Annamária ,  Kovács Éva ,  Kovács M. ,  Krausz T. ,  Litkei G. ,  Lovász A. ,  Mátrai Gizella ,  Miklós D. ,  Münnich Á. ,  Nagy János ,  Németh Imre (Celldömölk) ,  Orosz Á. ,  Páles Zs. ,  Rapp F. ,  Ruppert L. ,  Sárga E. ,  Smohay T. ,  Sparing L. ,  Sramó A. ,  Szathmári A. ,  Szép J. ,  Tornóci L. ,  Udvardy Magdolna ,  Varga B. ,  Varga Erzsébet ,  Vass Albert (Debrecen) ,  Veres S. ,  Werderits F. 
Füzet: 1974/szeptember, 11 - 12. oldal  PDF  |  MathML 
Témakör(ök): Hozzáírt körök, Paralelogrammák, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):Feladatok: 1973/december: F.1909

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A paralelogrammákban AD#BC#EA (az irányt is beleértve), tehát D és E egymás tükörképei A-ra mint centrumra.
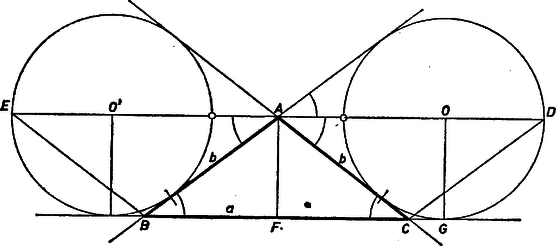
A két kör bele van írva a BAC (180∘-nál kisebb) szögtartománynak abba a két mellékszögtartományába, amely vele az AB, illetve AC félegyenes mentén szomszédos; e két tartomány egymásnak csúcsszögtartománya. Így a két kör egymás képe egy A centrumú, valamilyen arányú hasonlósági transzformációban, továbbá az előbbiek szerint az egymás meghosszabbítását adó AD, AE félegyenesek is egymás képei.

 

 

Az AD félegyenes a D-n átmenő hozzáírt kört másodszor A és D között metszi, mert az ellentétes esetben az ABCD paralelogrammának és a körnek D lenne az egyetlen közös pontja, így pedig a kör nem érinthetné a paralelogramma belsejében levő AC szakaszt. Ugyanígy E is A-tól távolabbi metszéspontja az AB oldalhoz hozzáírt körnek és az AE félegyenesnek.
Ezek szerint a D és E pontok is egymás megfelelői a mondott centrális hasonlóságban, tehát DA=EA alapján a nagyítási arány 1, a két kör sugara egyenlő. Ezért az O, O' középpontjaikat összekötő egyenes párhuzamos BC-vel, másrészt áthalad A-n, hiszen ez az egyenes a háromszög A-nál levő külső szögeinek a felezője, és ezen van D is, E is. Így a félszögek váltószögeiként ABC∢=ACB∢, az ABC háromszög egyenlő szárú: AB=AC, szögeinek kiszámításához elég meghatároznunk alapjának és szárának arányát.
Legyen a BC alap felezőpontja F, az AC oldalhoz hozzáírt kör érintési pontja a BC oldal meghosszabbításán G. Ekkor ‐ mint ismeretes ‐ BG egyenlő az ABC háromszög kerületének felével, és az oldalak, szögek szokásos jelöléseivel
a=BC=AD=AO+OD=FG+OG=(BG-BF)+AF=a+2b2-a2+b2-a24,(a-b)2=b2-a24,(a≠0)a/2b=cosβ=45,β=γ=36∘52',α=106∘16'.


Ezzel a megoldást befejeztük.
 

Megjegyzés. Szokás az ABCD paralelogramma D csúcsát az ABC háromszög (egyik) külső súlypontjának nevezni, ugyanis itt van a tömegpontrendszer súlypontja, ha A-ba és C-be (+1) tömeget és B-be (-1) tömeget gondolunk. Ebben a szóhasználatban a feladat föltevésének egyik része így mondható ki: a B-vel szemben fekvő oldalhoz hozzáírt külső érintő kör átmegy a B-vel szemben fekvő külső súlyponton.
Ezek után rámutathatunk a feladat eredetére. Lapunk 1966. évi pályázatának tárgya az olyan háromszögek több irányú vizsgálata volt, melyeknek beírt köre átmegy a súlyponton. Egy ilyen háromszöget vizsgált egy további érdekesség mellett az 1805. feladat, * és annak kapcsán merült fel az általánosítás kérdése, külső súlypontra, külső érintő körre. Ezúttal nem numerikus könnyítést vettünk, hanem egyenlő szárú háromszöget (két külső súlypont révén). ‐ Az érdeklődőknek ajánljuk a három oldal közti összefüggés megállapítását azzal a követeléssel, hogy a külső érintő körök egyike menjen át a megfelelő külső súlyponton.
*Megoldása: K. M. L. 45. (1972) 12.