Kezdőlap


Feladat:	F.1904	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1974/április, 154 - 156. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Négyszög alapú gúlák, Téglatest, Mértani helyek, Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1973/november: F.1904

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az $L_{i}$ lap egymás utáni csúcsai $A_{i}$ , $B_{i}$ , $C_{i}$ , $D_{i}$ $(i = 1, 2)$ és a téglatest éleinek hossza $A_{1} B_{1} = a$ , $A_{1} D_{1} = b$ , $A_{1} A_{2} = c$ . Mivel $L_{1}$ is, $L_{2}$ is önmagába megy át az $A_{2} B_{2}$ és az $A_{2} D_{2}$ él felező merőleges síkján való tükrözéssel, azért elég gúlánk felszínét addig vizsgálni, míg $M$ csúcsa bejárja $L_{2}$ kerületének negyedrészét, az $E A_{2}$ és $A_{2} F$ szakaszt, ahol $E$ az $A_{2} D_{2}$ él, $F$ pedig az $A_{2} B_{2}$ él felezőpontja. Sőt, minőségileg elég lesz az $A_{2} F$ szakaszra szorítkozni, mert az itt adódó eredményeink az $a$ , $b$ betűk cseréjével megadják az $A_{2} E$ szakaszon mozgó $M$ -re vonatkozó eredményeket.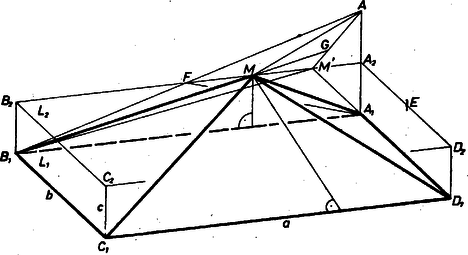

A felszín változásának vizsgálatában az állandó

L_{1}

alapot figyelmen kívül hagyhatjuk. Ugyanígy az

M A_{1} B_{1}

M C_{1} D_{1}

oldallapokat is, mert területük állandó, hiszen korlátozásunk szerint közös

M

csúcsuk az

A_{1} B_{1}

, illetőleg

C_{1} D_{1}

alapjukkal párhuzamos egyenesen mozog.
A változó területű

M A_{1} D_{1}

és

M B_{1} C_{1}

oldallapok együttes területéről megmutatjuk, hogy szigorúan monoton nő, míg

M

F

-től

A_{2}

-ig halad; így

M = F

esetén minimuma,

M = A_{2}

esetén maximuma van a gúla felszínének. Valóban, e két lap területének

2

-szerese

\begin{matrix} b \cdot M A_{1} + b \cdot M B_{1} = b (A_{1} M + M B_{1}) . \end{matrix}

hiszen e lapok

A_{1}

-nél, illetve

B_{1}

-nél levő szöge derékszög; így csak a zárójelbeli összeget kell vizsgálnunk. Legyen

A_{1}

-nek az

A_{2} B_{2}

egyenesre való tükörképe

A

, így

M

-nek minden tekintett helyzetében

\begin{matrix} A_{1} M + M B_{1} = A M + M B_{1} ≧ A B_{1} = A F + F B_{1} = A_{1} F + F B_{1}, \end{matrix}

és egyenlőség akkor és csakis akkor áll, ha

M

F

-ben van, hiszen

F

A B_{1}

szakaszt is felezi.
Ha mármost

M'

A_{2} M

szakasznak

M

-től különböző belső pontja és

A_{2} M < A_{2} F

, akkor a

B_{1} M

és

A M'

egyenesek

G

metszéspontja az

A M'

szakasznak,

M

pedig a

G B_{1}

szakasznak belső pontja, így a háromszög‐egyenlőtlenséget az

A M G

és

G B_{1} M'

háromszögekre alkalmazva

\begin{matrix} A_{1} M + M B_{1} = A M + M B_{1} < (A G + G M) + M B_{1} = A G + G B_{1} < A G + (G M' + M' B_{1}) = \\ = A M' + M' B_{1} = A_{1} M' + M' B_{1} . \end{matrix}

Ugyanezzel a meggondolással a jobb oldal kisebb, mint

A_{1} A_{2} + A_{2} B_{1}

, tehát a gúla csúcsát

M

-ből

M'

-be áttolva, a felszín valóban nő (nem is marad változatlanul). Ezzel állításunkat bebizonyítottuk.
Meg lehetne még vizsgálni, hogy a felszínnek

E

-ben és

F

-ben adódó lokális minimumai közül melyik a kisebb, az abszolút minimum. (Ezt a feladat előre nem kérdezte, nem kérdezhette; hiszen elébe vágott volna a föltett kérdés eredményének.) Nos, a palástfelszínek 2-szeresei, a gúla csúcsát

F

-ben,illetőleg

E

-ben választva így írhatók:

\begin{matrix} a c + \sqrt[]{a^{2} b^{2} + a^{2} c^{2}} + \sqrt[]{a^{2} b^{2} + 4 b^{2} c^{2}}, illetve \\ b c + \sqrt[]{a^{2} b^{2} + b^{2} c^{2}} + \sqrt[]{a^{2} b^{2} + 4 a^{2} c^{2}} . \end{matrix}

Eszerint nagyságviszonyuknak pl. az

a > b

föltevés mellett való megállapítása messze meghaladná azt a munkát, amit az alapfeladat megoldására végeztünk. Ezért megelégszünk a kérdés fölvetésével.

Megjegyzés. Az érkezett dolgozatok a változást a differenciálszámítás eljárásával vizsgálták, bár sokszor hiányosan. Vázoljuk ezt. Legyen a fenti jelölésekkel

A_{2} M = x

, ahol

0 ≦ x ≦ a

A felszín nem változó tagjait, majd a nem változó (pozitív) tényezőt elhagyva az

\begin{matrix} f (x) = A_{1} M + M B_{1} = \sqrt[]{x^{2} + c^{2}} + \sqrt[]{{(a - x)}^{2} + c^{2}} \end{matrix}

függvény deriváltja valamely

0 < x < a

helyen

\begin{matrix} f' (x) = \frac{x}{\sqrt[]{x^{2} + c^{2}}} - \frac{a - x}{\sqrt[]{{(a - x)}^{2} + c^{2}}} = \frac{1}{\sqrt[]{1 + {(\frac{c}{x})}^{2}}} - \frac{1}{\sqrt[]{1 + {(\frac{c}{a - x})}^{2}}}; \end{matrix}

Innen egyrészt nyilvánvaló, hogy

f' (x)

akkor és csakis akkor tűnik el, ha

x =

= a - x

, azaz

x = a / 2

, másrészt látjuk, hogy

0 < x < a / 2

mellett

f' (x) <

< 0

, hiszen az alakítás szerint első tagjának (pozitív) nevezője nagyobb, mint a második tag nevezője, tehát itt

f (x)

fogy, és hasonlóan

a / 2 < x < a

mellett nő, tehát az

x = a / 2

helyen minimuma van. [Az eredeti alakból az is látható, hogy

f' (x)

jobb oldali határértéke az

x = 0

helyen ugyancsak negatív, és bal oldali határértéke az

x = a

helyen ugyancsak pozitív.]