Kezdőlap


Feladat:	F.1896	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Böősi Imre
Füzet:	1979/december, 209 - 210. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Koszinusztétel alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1973/október: F.1896

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen adott az $A$ csúcsnál levő szög, $α$ . Rögzítsük a $B E$ súlyvonalat és tekintsük egységnyinek. Így a háromszög $A$ csúcsa egy olyan köríven mozoghat, ahonnan $B E$ $α$ szög alatt látszik (1. ábra). Ha az $A$ csúcs a $B E$ íven végigfut, az adott $α$ -val a hasonlóság erejéig minden háromszög létrejön, amelyet vizsgálnunk kell. Mivel $s_{b} = 1$ , az $\frac{s_{c}}{s_{b}}$ hányados minimuma, ill. maximuma helyett elég $s_{c}$ minimumát, ill. maximumát vizsgálnunk.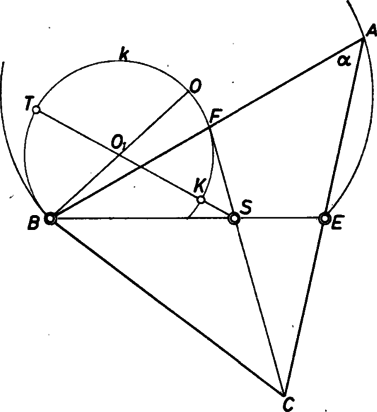

1. ábra

A B

minden helyzetében megrajzoljuk ennek felezőpontját,

F

-et, akkor egy olyan

k

látószög-körívet kapunk, amely az eredetiből

B

középpontú,

0, 5

arányú kicsinyítéssel származik. Az

s_{c}

akkor minimális, ill. maximális, amikor a harmadrésze,

S F

minimális, ill. maximális, ahol

S

A B C

háromszög súlypontja. Keressük tehát a

k

körívnek

S

-től mért legközelebbi

(K)

, illetve legtávolabbi

(T)

pontját.
Először foglalkozzunk az 1. ábrán vázolt esettel, azaz amikor

α

hegyesszög. Ekkor

K

és

T

S

pontot

k

O_{1}

középpontjával összekötő egyenesen van. A keresett határok, amelyek között

s_{c}

(és így jelen esetben

\frac{s_{c}}{s_{b}}

is) változhat:

3 \cdot S K

, ill.

3 \cdot S T

.
Jelöljük

B E

látókörének középpontját

O

-val. Mivel

B E = 1

, azért

O_{1} B = B O / 2 = B E / 4 sin α = 1 / 4 sin α

B S = 2 / 3

és

O_{1} B S ∢ = 90^{\circ} - α

. Az

O_{1} S

értékét a koszinusztételből számolhatjuk, és így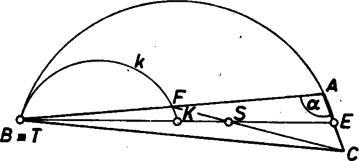

\begin{matrix} {(\frac{s_{c}}{s_{b}})}_{min} = 3 S K & = 3 (O_{1} S - O_{1} B) = \frac{- 3 + \sqrt[]{9 + 16 sin^{2} α}}{4 sin α}, \\ {(\frac{s_{c}}{s_{b}})}_{max} = 3 S T & = 3 (O_{1} S + O_{1} B) = \frac{3 + \sqrt[]{9 + 16 sin^{2} α}}{4 sin α} . \end{matrix}

2. ábra

3. ábra

α \geq 90^{\circ}

(2. és 3. ábra), akkor

k S

-től mért legközelebbi és legtávolabbi pontja a

B E

szakaszon van,

K

B E

felezőpontja,

T

pedig azonos

B

-vel. Ekkor

3 \cdot S K = 1 / 2

3 \cdot S T = 2

.
A súlyvonalak aránya tehát most

\frac{1}{2}

és

2

között változhat. Megjegyezzük hogy az

\frac{1}{2}

és

2

értékek itt csak elfajuló

A B C

háromszögekben jöhetnek létre, míg

α < 90^{\circ}

esetén az ott kapott szélsőértékek valódi

A B C

háromszögekben valósulnak meg, s ezek

\frac{1}{2}

-nél kisebb, ill.

2

-nél nagyobb értékek. L.L.

Böősi Imre (Győr, Czuczor G. Bencés Gimn.)