Kezdőlap


Feladat:	F.1879	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1976/november, 111 - 113. oldal		PDF \| MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Síkgeometriai szerkesztések, Ellipszis, mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1973/április: F.1879

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Vizsgáljuk meg először, mi jellemzi az ellipszis érintőit. Az ellipszisnek a következő definícióját használjuk: ha adottak a síkon a (nem feltétlenül különböző) $F_{1}, F_{2}$ pontok, és adott egy $2 a$ hosszúságú szakasz, a sík azon $P$ pontjainak a mértani helye, amelyekre

\begin{matrix} F_{1} P + P F_{2} = 2 a, \end{matrix}

(1)

F_{1}, F_{2}

fókuszú,

2 a

nagytengelyű ellipszis. Ilyen pontok nyilván csak akkor vannak, ha

2 a > F_{1} F_{2}

. Jelöljük

F_{1} F_{2}

hosszát

2 c

-vel. A sík azon

Q

pontjai, amelyekre

\begin{matrix} F_{1} Q + Q F_{2} < 2 a, \end{matrix}

(2)

az ellipszis belsejéhez tartoznak. Könnyen ellenőrizhető, hogy az ellipszis belseje bármely két pontjával azok összekötő szakaszát is tartalmazza. Emiatt azt mondjuk, hogy az ellipszis konvex görbe. Konvex görbék adott

P

pontbeli érintőjét definiálhatjuk a következő módon: azt mondjuk, hogy a

P

-n átmenő

e

egyenes érinti a görbét, ha

e

-nek nincs a görbe belsejéhez tartozó pontja, de bármely más,

P

-n átmenő egyenesen van a görbe belsejéhez tartozó pont.
Mivel az

F_{1} F_{2}

szakasz tetszőleges

Q

pontjára

F_{1} Q + Q F_{2} = F_{1} F_{2} < 2 a

, ha egy egyenes metszi az

F_{1} F_{2}

szakaszt, nem érintheti az ellipszist. Legyen

e

tetszőleges, az

F_{1} F_{2}

szakaszt nem metsző egyenes, és legyen az

F_{1}, F_{2}

pontok

e

-n levő vetülete

T_{1}, T_{2}

, az

F_{1} F_{2}

szakasz

C

felezőpontjának

e

-n levő vetülete pedig

T

(1. ábra).

1. ábra

Mivel

T

felezi a

T_{1} T_{2}

szakaszt,

C

T_{1}, T_{2}

pontoktól egyenlő távolságra van, azaz

C T_{1} = C T_{2}

. Megmutatjuk, hogy

e

akkor és csakis akkor érinti az

F_{1}, F_{2}

fókuszú,

2 a

nagytengelyű ellipszist, ha

\begin{matrix} C T_{1} = C T_{2} = a . \end{matrix}

(3)

Legyen

F_{2}

-nek

e

-re vonatkozó tükörképe

F'_{2}

. Mivel

e

nem metszi az

F_{1} F_{2}

szakaszt, biztosan metszi az

F_{1} F'_{2}

szakaszt, jelöljük a metszéspontot

P

-vel. Felhasználva, hogy

C T_{2}

F_{1} F_{2} F'_{2}

háromszög középvonala, kapjuk, hogy

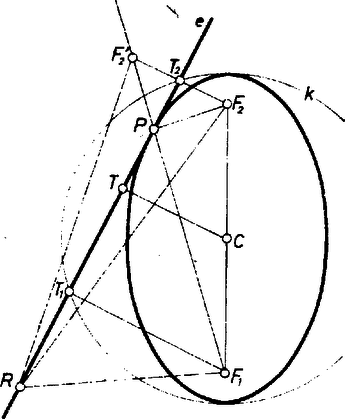\begin{matrix} F_{1} P + P F_{2} = F_{1} P + P F'_{2} = F_{1} F'_{2} = 2 C T_{2}, \end{matrix}

(4)

ha pedig

R

e

egyenes tetszőleges,

P

-től különböző pontja, akkor

\begin{matrix} F_{1} R + R F_{2} = F_{1} R + R F'_{2} > F_{1} F'_{2} = 2 C T_{2} . \end{matrix}

(5)

A kapott (4) és (5) összefüggések együtt azt jelentik, hogy az

F_{1} R + R F_{2}

összeg az

e

pontjai közül

P

-re minimális. Ha tehát

e

érinti az ellipszist, az érintési pont csak

P

lehet, és így (4) miatt teljesül (3). Ha pedig

e

-re teljesül (3), akkor (4) miatt

P

az ellipszisen van, és (5) miatt

e

-n nincs az ellipszisnek belső pontja. Tetszőleges más,

P

-n átmenő egyenesre viszont nem

P

-ben lesz az

F_{1} R + R F_{2}

összeg minimális, van tehát az egyenesen olyan

Q

pont, amelyre

\begin{matrix} F_{1} Q + Q F_{2} < F_{1} P + P F_{2} = 2 a, \end{matrix}

vagyis

Q

az ellipszis belső pontja.
A

C

körül

a

sugárral rajzolt

k

kört az ellipszis főkörének nevezik. A most bizonyított állítás szavakban a következőket jelenti:

a)

Ha valamely egyenes érint egy ellipszist, akkor az ellipszis fókuszainak az egyenesen levő vetületei az ellipszis főkörén vannak.

b)

Ha az ellipszis egyik fókuszának egy tetszőleges egyenesen levő vetülete az ellipszis főkörén van, akkor ugyancsak a főkörön van a másik fókusznak az egyenesen levő vetülete is, és az egyenes érinti az ellipszist.
2. Rátérünk a feladatban mondott mértani hely vizsgálatára. Jelöljük a derékszög szárait

e'

-vel,

e''

-vel, csúcsát

O

-val, az ellipszis egy tetszőleges, a feladatban mondott mozgása során felvett helyzetében a fókuszok legyenek

F_{1}

és

F_{2}

, az

F_{1} F_{2}

felezőpontja

C

, a

C

körüli

a

sugarú kör

k

, az

F_{1}, F_{2}

pontok

e'

-n, illetve

e''

-n levő vetületei

T'_{1}, T'_{2}

, illetve

T''_{1}, T''_{2}

(2. ábra).

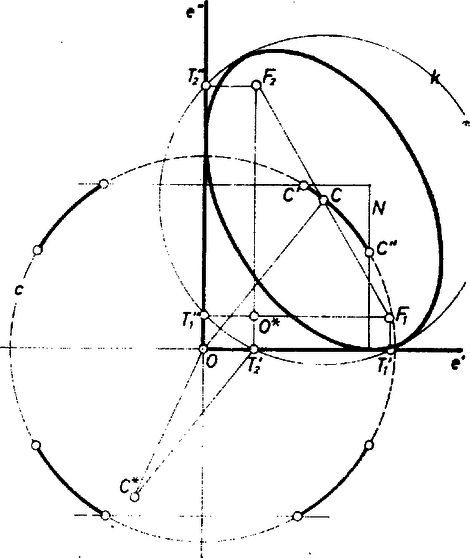2. ábra

a)

állítás szerint a

T'_{1}, T'_{2}, T''_{1}, T''_{2}

pontok

k

-n vannak. Jelöljük a

C, O

pontoknak a

T''_{1} T'_{2}

szakasz felezőpontjára vonatkozó tükörképét

C^{*}

-gal,

O^{*}

-gal. Ismeretes, hogy egy paralelogrammában az átlók négyzetösszege egyenlő az oldalak négyzetösszegével. Emiatt

\begin{matrix} 2 (C O^{2} + C O^{* 2}) = O O^{* 2} + C C^{* 2} \\ 2 (C T_{1}^{'' 2} + C T_{2}^{' 2}) = T''_{1} T_{2}^{' 2} + C C^{* 2} . \end{matrix}

Mivel

O O^{*} = T''_{1} T'_{2}

, és

C T''_{1} = C T'_{2} = a, C O^{*} = C F_{1} = c

, ebből kapjuk, hogy

\begin{matrix} C O^{2} = 2 a^{2} - C F_{1}^{2}, \end{matrix}

(6)

vagyis

C

rajta van az

O

középpontú,

r = \sqrt[]{2 a^{2} - c^{2}}

sugarú

c

körön. Mivel a

C

középpontú,

a

sugarú

k

kör metszi

e', e''

egyeneseket,

C

egyik egyenestől sem lehet

a

-nál távolabb. Jelöljük a vizsgált síknegyedben levő, az

e', e''

egyenesekre támaszkodó

a

oldalú négyzetet

N

-nel,

c

-nek

N

határán levő pontjait

C'

-vel,

C''

-vel. Beláttuk, hogy a vizsgált mértani hely pontjai rajta vannak a

c

kör

N

-beli

C' C''

ívén.
3. Megmutatjuk, hogy a

c

kör

N

-beli

C' C''

ívének tetszőleges

C

pontja (a

C', C''

pontokat is beleértve) a vizsgált mértani helyhez tartozik. Mivel

C

N

-ben van, a

C

középpontú,

a

sugarú

k

kör metszi az

e', e''

egyeneseket, a metszéspontokat jelöljük

T'_{1}

-vel,

T'_{2}

-vel, illetve

T''_{1}

-vel,

T''_{2}

-vel, és legyen

F_{1}

, illetve

F_{2}

az a pont, melynek

T'_{1}, T''_{1}

, illetve

T'_{2}, T''_{2}

e', e''

egyeneseken levő vetülete (ha

e'

vagy

e''

érinti

k

-t,

T'_{1}

és

T'_{2}

vagy

T''_{1}

és

T''_{2}

azonosak). Mivel (6) most is igaz,

C F_{1}^{2} = 2 a^{2} - C O^{2} = c^{2}

, vagyis az

F_{1}, F_{2}

pontok távolsága megegyezik a mozgatott ellipszis fókuszainak a távolságával. Mivel az

F_{1}, F_{2}

pontoknak az

e', e''

egyeneseken levő vetülete rajta van a

C

középpontú,

a

sugarú körön, a

b)

állítás szerint ezek az egyenesek érintik az

F_{1}, F_{2}

fókuszú,

2 a

nagytengelyű ellipszist.

C

tehát valóban a vizsgált mértani helyhez tartozik.
4. Ha

k

nem érinti az

e', e''

egyeneseket, a metszéspontok betűzésének megválasztásától függően két különböző helyzetet kapunk az

F_{1}, F_{2}

fókuszokra, ezek a helyzetek a

C

-n átmenő, az

e', e''

egyenesekkel párhuzamos tengelyekre nézve szimmetrikusan helyezkednek el. Ha nemcsak egy síknegyedre szorítkozunk, a vizsgált mértani hely darabjait a

C' C''

ívnek az

e', e''

egyenesekre, illetve az

O

pontra való tükrözésével kaphatjuk meg.

Megjegyzés. Feladatunk szoros kapcsolatban van a később kitűzött 1958. feladattal. ^{$^{*}$} Állítsunk ugyanis a térben a mozgatott ellipszis fölé annak minden helyzetében olyan kört, amely érinti az ellipszis síkját, és amelynek épp az ellipszis a vetülete. Ez a kör érinti az ellipszis síkjára merőleges, azt az

e', e''

egyenesekben metsző síkokat is, tehát az 1958. feladat állítása szerint a középpontja rajta van az

O

középpontú,

\sqrt[]{2} a

sugarú gömbön. Mivel a kör alapsíkon levő vetületében a kis- és nagytengely aránya állandó, mozgása közben a kör az alapsíkkal állandó szöget zár be, tehát a középpontja az alapsíktól állandó távolságra van. Emiatt a középpont a rendelkezésre álló gömb helyett annak csak egy körvonalán mozog, és a minket érdeklő mértani hely ennek az alapsíkon levő vetülete.

^{$^{*}$}Megoldása megjelent a KÖMAL 1975/5. szám (50. kötet) 206‐207. oldalán.