Kezdőlap


Feladat:	F.1878	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bezdek K. , Borbély A. , Braun J. , Cséplő G. , Czompó J. , Fazekas l. , Horváth O. , Iszlay Z. , Katona Klára , Kiss E. , Kiss Rozália , Lakner P. , Leicht G. , Meszéna G. , Orosz Á. , Páles Zs. , Pálfalvi Gy. , Rapp F. , Veres S. , Vladár K.
Füzet:	1974/május, 197 - 201. oldal		PDF \| MathML
Témakör(ök):	Ceva-tétel, Menelaosz-tétel, Hossz, kerület, Projektív geometria, Párhuzamos szelők tétele, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül, Vektorok lineáris kombinációi, Feladat
Hivatkozás(ok):	Feladatok: 1973/április: F.1878

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A jelzőrudak letűzésére mondottak szerint az $R_{1}, ..., R_{6}$ pontok mindegyike létrejött. Föltesszük, hogy $R_{2}$ az $R_{1}$ -től is, $R_{3}$ -tól is különböző, így a további pontok is különbözők.
1. Húzzunk párhuzamost $R_{3}$ -on át $A R_{1}$ -gyel és jelöljük $A B$ -vel való metszéspontját $S$ -sel.

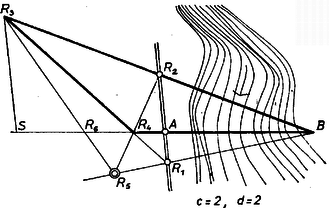1. ábra

Ekkor a párhuzamos szelők tételei alapján

\begin{matrix} egyrészt \frac{R_{4} R_{1}}{R_{1} R_{3}} = \frac{R_{4} A}{A S}, másrészt \frac{R_{3} R_{2}}{R_{2} B} = \frac{S A}{A B} . \end{matrix}

Írjuk fel még a következő azonosságot:

\begin{matrix} \frac{B A}{A R_{4}} = \frac{B A}{A R_{4}}, \end{matrix}

szorozzuk össze e három egyenlőség bal, illetve jobb oldalait, és változtassuk meg a jobb oldalon a nevező tényezőinek sorrendjét az alábbiak szerint:

\begin{matrix} \frac{B A}{A R_{4}} \cdot \frac{R_{4} R_{1}}{R_{1} R_{3}} \cdot \frac{R_{3} R_{2}}{R_{2} B} & = \frac{B A \cdot R_{4} A \cdot S A}{A R_{4} \cdot A S \cdot A B} = & (1) \\ = \frac{B A}{A B} \cdot \frac{R_{4} A}{A R_{4}} \cdot \frac{S A}{A S} (= - 1) . \end{matrix}

Ezt az összefüggést ismételten fel fogjuk használni, ezért továbbhaladás előtt értelmezni fogjuk. Ha az

A B

egyenesen valamelyik irányt pozitívnak, a vele ellentétes irányt negatívnak vesszük, akkor a jobb oldal értéke

(- 1)

, hiszen mindhárom tényezője

(- 1)

.
A bal oldalt értelmezzük így: a

B R_{4} R_{3}

háromszöget átmetszettük az

A R_{1} R_{2}

egyenessel, vettük a háromszög

B R_{4}

R_{4} R_{3}

R_{3} B

oldalegyenesén rendre adódott

A

R_{1}

R_{2}

metszésponttól az illető oldalszakasz végpontjaiig terjedő szakaszok arányát, majd e

3

arány szorzatát.

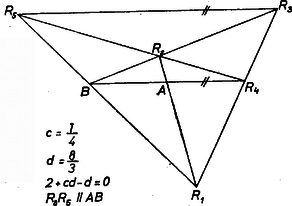2. ábra

Az egyes oldalegyeneseken levő két szakaszból úgy képeztük az arányt, hogy a háromszög oldalait a csúcsok

B

R_{4}

R_{2}

sorrendjében jártuk be, és mindegyik egyenesen a kezdőponttól a metszéspontig terjedő szakaszt osztottuk a metszésponttól a végpontig terjedő szakasszal. Így ábránk esetében az

R_{4} R_{1}

szakasz a menetiránnyal ellentétes, ezért negatívnak vesszük, a többi

5

szakasz pozitív, megegyezésben a jobb oldal

(- 1)

-es értékével.
Eredményünk természetesen bármely háromszögnek bármely egyenessel való átmetszésére érvényes, hacsak az egyenes nem megy át a háromszög egyik csúcsán sem. Az összefüggést Menelaos tételének nevezik.
2. Alkalmazzuk Menelaos tételét az

R_{5} R_{4}

egyenessel kettévágott

B R_{4} R_{3}

háromszög

R_{4} R_{2} B

és

R_{4} R_{2} R_{3}

részeire, szelőnek az első részháromszög esetében az

R_{5} R_{3}

egyenest véve, a másodikéban az

R_{5} B

-t:

\begin{matrix} \frac{R_{4} R_{5}}{R_{5} R_{2}} \cdot \frac{R_{2} R_{3}}{R_{3} B} \cdot \frac{B R_{6}}{R_{6} R_{4}} = - 1, \frac{R_{4} R_{5}}{R_{5} R_{2}} \cdot \frac{R_{2} B}{B R_{3}} \cdot \frac{R_{3} R_{1}}{R_{1} R_{4}} = - 1. \end{matrix}

Az előbbit az utóbbival osztva, valamint négy szakaszt a

(- 1)

-szeresével pótolva, egyszerűsítve

\begin{matrix} \frac{B R_{6}}{R_{6} R_{4}} \cdot \frac{R_{4} R_{1}}{R_{1} R_{3}} \cdot \frac{R_{3} R_{2}}{R_{2} B} = 1. \end{matrix}

(2)

(Ezt az összefüggést általános érvénnyel az 1. megjegyzésben értelmezzük.)
Képezve (1) és (2) hányadosát, a 2. és 3. arányok hányadosa

1

, így

\begin{matrix} \frac{B A}{A R_{4}} \cdot \frac{R_{6} R_{4}}{B R_{6}} = - 1, \end{matrix}

(3)

és itt mindegyik szakasz az

A B

egyenesnek a része, mérhető, ill. kifejezhető az

A B

ismeretlennel:

B R_{6} = B A \pm A R_{6}

, így az egyismeretlenes egyenletből

\begin{matrix} B A = \frac{\mp A R_{4} \cdot A R_{6}}{R_{6} R_{4} - A R_{4}}, | B A | = \frac{A R_{4} \cdot A R_{6}}{| A R_{4} - R_{4} R_{6} |}, \end{matrix}

amit bizonyítanunk kellett.

Megjegyzések. 1. A (2) összefüggést (Ceva tétele) így értelmezzük: a

B R_{4} R_{3}

háromszög oldalegyeneseinek, valamint a síkja

R_{5}

pontját a csúcsokkal összekötő egyeneseknek metszéspontját rendre

R_{6}

-tal,

R_{1}

-gyel,

R_{2}

-vel jelölve, az oldalakon keletkezett szakaszpárokból képezett arányok szorzata

1

, a szakaszok sorrendjét, irányát ugyanúgy értve, mint a Menelaos-tétel esetében.
2. Akik foglalkoztak az ún. projektív geometria elemeivel,^{$^{*}$} azok bizonyára fölismerik: az

R_{1}, ..., R_{6}

pontokat úgy jelöltük ki, hogy

B

és

R_{4}

R_{1}

R_{2}

R_{3}

és

R_{5}

pontokkal meghatározott teljes négyszögnek ún. átlós pontjai legyenek. Így a

B R_{4}

egyenes a teljes négyszög egymással szemben fekvő

R_{1} R_{2}

és

R_{3} R_{5}

oldalegyeneseit az

A

R_{6}

pontokban metszi, és az erre az alakzatra vonatkozó alaptétel szerint a

B

R_{4}

és

A

R_{6}

pontpárok harmonikusan választják szét egymást, amin ezt értjük:

\begin{matrix} (\frac{B A}{A R_{4}}) : (\frac{B R_{6}}{R_{6} R_{4}}) = - 1. \end{matrix}

(A teljes négyszögnek

6

oldalegyenese van, bármelyik

2

csúcsát összekötő egyenesét oldalegyenesének nevezzük, továbbá

3

átlós pontja, amelyekben

2 - 2

szemben fekvő (közös csúcsot nem tartalmazó) oldalegyenes metszi egymást.) ‐ Ezek ismeretében azonnal felírhattuk volna (3)-at. ‐ Az eljárás kidolgozói természetesen ismerték ezt a hátteret.

II. megoldás. Vektorok felhasználásával bizonyítjuk az állítást. Legyen

\begin{matrix} \vec{B A} = a, \vec{A R_{1}} = r, \vec{A R_{2}} = - c r, \\ \vec{B R_{3}} = d \cdot \vec{B R_{2}} = d (a - c r), \end{matrix}

ahol

r

nem párhuzamos

a

-val,

c

és

d

számok,

c \neq 0

és

c \neq 1

, illetve

d > 0

és

d \neq 1

. Így az

R_{1} R_{3}

egyenes tetszőleges

X

pontjára valamely

e

számmal

\begin{matrix} \vec{B X} & = {\vec{B R}}_{1} + {\vec{e R_{1} R}}_{3} = {\vec{B R}}_{1} + e ({\vec{B R}}_{3} - {\vec{B R}}_{1}) = \\ = (1 - e) {\vec{B R}}_{1} + e {\vec{B R}}_{3} = (1 - e) (a + r) + d e (a - c r) = \\ = (1 - e + d e) a + (1 - e - c d e) r . \end{matrix}

X

akkor és csak akkor azonos

R_{4}

-gyel, ha a

\vec{B X}

egyirányú a

\vec{B A}

-ral, vagyis

r

együtthatója

0

\begin{matrix} 1 - e - c d e = 0, tehát e = \frac{1}{1 + c d}, \end{matrix}

és ekkor

\begin{matrix} {\vec{B R}}_{4} = \frac{(c + l) d}{1 + c d} a, \end{matrix}

hacsak

c d \neq - 1

. A

c d = - 1

értéket a jelzőrudak helyzetére tett föltevések kizárják. Ekkor ugyanis

d > 0

miatt

c < 0

R_{2}

ugyanazon az oldalán van

A B

-nek, mint

R_{1}

, az

R_{3}

-on átmenő,

A R_{1}

-gyel párhuzamos egyenesnek

R_{3}

-tól

A B

-ig terjedő

R_{3} Q

szakasza

R_{3} Q = d \cdot R_{2} A = d \cdot | c | \cdot R_{1} A = R_{1} A

, tehát

R_{1} R_{3}

párhuzamos

A B

-vel,

R_{4}

nem jön létre.
Hasonlóan az

R_{2} R_{4}

egyenes bármely

X

pontjára valamely

f

számmal

\begin{matrix} \vec{B X} & = {\vec{B R}}_{2} + f \cdot \vec{R_{2} R_{4}} = (1 - f) \vec{B R_{2}} + f \cdot \vec{B R_{4}} = \\ = (1 - f + \frac{(c + 1) d f}{1 + c d}) a - c (1 - f) r, \end{matrix}

és

X

arra és csak arra az

f

-re azonos

R_{5}

-tel, amelyre egy alkalmas

g

számmal

\begin{matrix} \vec{B X} = g \vec{B R_{1}} = g a + g r, \end{matrix}

azaz

\begin{matrix} g = 1 - f + \frac{(c + 1) d f}{1 + c d} = - c (1 - f) . \end{matrix}

Innen

c + 1 \neq 0

figyelembevételével

\begin{matrix} f = \frac{1 + c d}{1 + c d - d}, \vec{B R_{5}} = \frac{c d}{1 + c d - d} (a+r), \end{matrix}

hacsak

1 + c d - d \neq 0

. Az ellentétes esetben az

R_{2} R_{4}

egyenesen nem volna olyan

X

, melyre

B X

párhuzamos volna

B R_{1}

-gyel, tehát

R_{2} R_{4} | | B R_{1}

lenne, nem lenne

R_{5}

, és ezt kizártuk.
Végül az

R_{3} R_{5}

egyenes bármely

X

pontjára valamely

h

számmal

\begin{matrix} \vec{B X} = B R_{3} + h \cdot {\vec{R_{3} R}}_{5} = d (1 - h + \frac{c h}{1 + c d - d}) a + c d (h - 1 + \frac{h}{1 + c d - d}) r, \end{matrix}

és

X

akkor és csak akkor azonos

R_{6}

-tal, ha

r

együtthatója

0

, azaz

\begin{matrix} h = \frac{1 + c d - d}{2 + c d - d}, és így {\vec{B R}}_{6} = \frac{(c + 1) d}{2 c d - d} a. \end{matrix}

(A fentebbiekhez hasonlóan belátható, hogyha

2 + c d - d = 0

, akkor

R_{6}

nem jön létre, 2. ábra.)
Mármost eredményeinkből az állításban szereplő szakaszok hossza

\begin{matrix} A R_{4} = \frac{d - 1}{1 + c d} | a |, A R_{6} = \frac{2 (d - 1)}{2 + c d - d} | a |, \\ | R_{4} R_{6} - A R_{4} | = | A R_{6} - 2 A R_{4} | = \frac{2 {(d - 1)}^{2}}{(1 + c d) (2 + c d - d)} | a |, \end{matrix}

és ezek szerint az (1) kifejezés abszolút értéke

| a | = A B

, amint azt bizonyítanunk kellett.

^{$^{*}$} Lásd pl.: Vigassy Lajos: Projektív geometria (Középiskolai Szakköri Füzetek), Tankönyvkiadó, Budapest, 1970.