| Feladat: | F.1877 | Korcsoport: 16-17 | Nehézségi fok: - |
| Megoldó(k): | Bara T. , Bartha M. , Bezdek K. , Bogyó I. , Borbély A. , Cséplő G. , Dobor T. , Fazekas l. , Frankó F. , Fukker B. , Fördős J. A. , Hargitai B. , Horváth O. , Illés G. , Juhász I. , Kalmár J. , Katona Klára , Kelemen D. , Kiss E. , Kovács S. , Lakner P. , Lövei P. , Maczák Johanna , Meszéna G. , Molnár Gy. , Orosz Á. , Páles Zs. , Pócsi Gy. , Rapp F. , Remsei F. , Schvarcz T. , Seress Á. , Simányi N. , Surján P. , Sövér F. , Takács Judit , Terlaky T. , Tóth A. , Tóth Mária , Ureczky J. , Uzonyi Gy. , Veres S. , Vladár K. | ||
| Füzet: | 1974/április, 145 - 147. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Geometriai egyenlőtlenségek, Vetítések, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1973/április: F.1877 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Mondjuk azt, hogy a vizsgált terep rajzát úgy helyeztük magunk elé, hogy azon az autóutak közül az egyik fent van, a másik lent, és legyen az öt állomás balról jobbra haladva , , , , . Három útrendszert tervezünk. Az elsőben -n és -n át vezetünk egy‐egy függőleges 10 km-es utat, és -ből az elsőig, -ből, -ből a másodikig vezetünk vízszintes útszakaszokat (1. ábra). 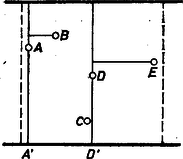 1. ábra A másodikban -n és -n át futnak a függőleges utak, és -t, -t az elsőhöz, -t a másodikhoz kötjük vízszintes utakkal (2. ábra). 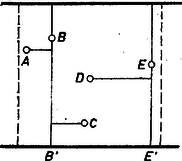 2. ábra A harmadikban csak egy függőleges út van, a -n átmenő, ehhez kötjük a többi pontot vízszintes utakkal. 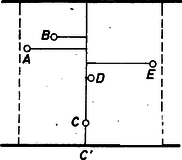 3. ábra A három útrendszerben együtt öt függőleges út van, ezek együttes hossza 50 km. Vetítsük le az alsó autópályára a pontokat, és jelöljük a vetületeket -vel, -vel, -vel, -vel és -vel (egybeesés természetesen lehetséges). A három útrendszer egyesítéséből kapott úthálózatban az , , , , szakaszok mindegyike felett három‐három vízszintes út halad, a vízszintes utak összhossza tehát egyenlő az szakasz hosszának a háromszorosával, ami legfeljebb 30 km. A három útrendszer összhossza ezek szerint legfeljebb 80 km, így közülük a legrövidebbik legfeljebb km. Ekkora összúthossz tehát mindig elegendő. 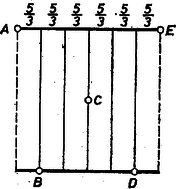 4. ábra Megmutatjuk, hogy a 4. ábra elrendezése mellett szükség is van km-es úthálózatra. Tetszőleges úthálózat alapján csoportosítsuk a pontokat úgy, hogy egy‐egy csoportba olyan pontok kerüljenek, amelyek közül bármelyikből bármelyikbe eljuthatunk kerékpáron. Ha így legalább három csoportot kapunk, az összhossz legalább 30 km, hiszen mindegyik csoporthoz legalább 10 km hosszú út tartozik, és ezeknek nincs közös darabja. Ha két csoport van, az úthálózathoz tartozó függőleges útdarabok összhossza legalább 20 km. A vízszintes útdarabok összege pedig legalább a csoportok pontjainak a vetületei között fellépő legnagyobb távolságok összegével egyenlő. Ha a (nagyobb) csoportban 4 pont van, ez legalább annyi, mint , ami km, ha 3, akkor ez legalább km. Az összhossz mindkét esetben legalább km. Az olyan úthálózatokban, amelyekben a pontok egy csoportot alkotnak, tekintsük az -ból -be és -ből -be vivő utakat (vagy ha több ilyen van, ezek egyikét). Ezek szükségszerűen keresztezik egymást, jelöljük -vel azt a pontot, ahol -ból felé haladva először érjük el a utat, és jelöljük -val azt a pontot, ahol azt végleg elhagyjuk. Ha -ből -be menve előbb -be jutunk, akkor az , útdaraboknak nincs közös pontja, tehát függőleges darabjaik összhossza legalább 20 km, amihez legalább -nyi vízszintes darabok csatlakoznak, és az együtt legalább 30 km (5. ábra). 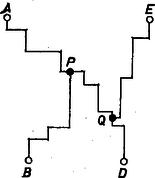 5. ábra Ha és azonos, vagy a után van a úton, akkor az , utaknak nincs közös vízszintes darabjuk, tehát az útrendszer vízszintes darabjainak az összhossza legalább km, ami a függőleges darabok legalább 10 kilométernyi összhosszával együtt legalább km. Megjegyzés. A feladat az 1972. évi Kürschák‐verseny egyik feladatának az általánosításával kapcsolatos. Ennek megfelelően a feladat kitűzésekor a szerkesztőség utalt a következő cikkre: Surányi János: Az 1972. évi Kürschák József matematikai tanulóverseny feladatainak megoldása, K.M.L. 46 (1973) 49‐57. old., élesebben 53‐57. oldal. A fenti megoldás a Kürschák‐verseny feladatának idézett egyik megoldásából úgy származtatható, hogy az eredeti megoldás minden olyan meggondolását, amely kihasználja, hogy éppen 4 megfigyelőállomás van, egy olyan meggondolással helyettesítettük, amelyik a kívánt eredményt 5 állomás esetére biztosítja. Tanulságos lehet a két megoldás összehasonlítása ebből a szempontból. |