Kezdőlap


Feladat:	F.1867	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Burda Magdolna
Füzet:	1973/október, 55 - 58. oldal		PDF \| MathML
Témakör(ök):	Merőleges affinitás, Derékszögű háromszögek geometriája, Egyenesek egyenlete, Ellipszis egyenlete, Négyzetek, Négyszögek szerkesztése, Síkgeometriai szerkesztések, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1973/február: F.1867

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az ellipszis szimmetriatengelyeit véve koordinátatengelyeknek, egyenlete a szokásos jelölésekkel

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1. \end{matrix}

(1)

Itt

b < a

, hiszen

b = a

esetén vonalunk körré specializálódik, márpedig kör köré írt négyzet szerkesztésével nem érdemes foglalkozni. Így a tengelyvégpontokbeli érintők különböző oldalú téglalapot alkotnak, tehát a szerkesztendő négyzet oldalegyeneseinek az ellipszissel való érintkezési pontjai nem eshetnek egyik adott tengelyvégpontba sem, a kívánt négyzet oldalai nem párhuzamosak a tengelyekkel.
Ismeretes,^{$^{*}$} hogy (1)-hez az

(x_{1}, y_{1})

pontjában húzott érintő egyenlete

\begin{matrix} \frac{x_{1} x}{a^{2}} + \frac{y_{1} y}{b^{2}} = 1, \end{matrix}

(1a)

‐ és számunkra

x_{1} \neq 0

és

y_{1} \neq 0

‐, tehát iránytangensét

m

-mel jelölve

\begin{matrix} m = \frac{b^{2} x_{1}}{a^{2} y_{1}} = - \frac{b x_{1}}{a \sqrt[]{a^{2} - x_{1}^{2}}} . \end{matrix}

Fordítva, az érintési pont koordinátái

m

függvényeként:

\begin{matrix} x_{1} = \pm \frac{a^{2} m}{\sqrt[]{a^{2} m^{2} + b^{2}}}, y_{1} = - \frac{b^{2} x_{1}}{a^{2} m} = \mp \frac{b^{2}}{\sqrt[]{a^{2} m^{2} + b^{2}}} . \end{matrix}

(2)

Eszerint adott

m

értéket két pontban ér el az iránytangens és e pontok egymás tükörképei az

O

centrumra. Az ellipszis szimmetriája alapján ugyanez áll a bennük megrajzolt érintőkre is, így tehát

O

a körülírt négyzetnek is középpontja lesz, a négyzet szomszédos oldalegyenespárjait tehát azzal jellemezhetjük, hogy merőlegesek egymásra és hogy

O

-tól mért távolságuk egyenlő.
Az érintő derékszögű háromszöget vág le abból a síknegyedből, amelyikben

(x_{1}, y_{1})

van, e háromszög befogói a tengelyekből lemetszett darabok, hosszuk (1a) alapján, majd (2) felhasználásával

\begin{matrix} e = | \frac{a^{2}}{x_{1}} | = \frac{\sqrt[]{a^{2} m^{2} + b^{2}}}{| m |}, f = | \frac{b^{2}}{y_{1}} | = \sqrt[]{a^{2} m^{2} + b^{2}}, \end{matrix}

(3)

ezekből az érintőnek

O

-tól mért távolsága mint az átfogóhoz tartozó magasság

\begin{matrix} \frac{e f}{\sqrt[]{e^{2} + f^{2}}} = \sqrt[]{\frac{a^{2} m^{2} + b^{2}}{1 + m^{2}}} . \end{matrix}

A másik oldalegyenespár

O

-tól mért távolságát úgy kapjuk ebből, hogy

m

helyére

- 1 / m

-ot írunk. Így a követelmény, mindjárt a távolságok négyzetének egyenlőségét felírva:

\begin{matrix} \frac{\frac{a^{2}}{m^{2}} + b^{2}}{1 + \frac{1}{m^{2}}} = \frac{a^{2} m^{2} + b^{2}}{1 + m^{2}}, \end{matrix}

átrendezve

\begin{matrix} (a^{2} - b^{2}) (1 - m^{2}) = 0. \end{matrix}

a \neq b

miatt csak

m \pm 1

mellett teljesül, tehát a kívánt négyzet oldalegyenesei

45^{\circ}

-os szöggel hajolnak a koordinátatengelyekhez.
Most már (2), majd (3) alapján

m = + 1

mellett

\begin{matrix} x_{1} = \pm \frac{a^{2}}{\sqrt[]{a^{2} + b^{2}}}, y_{1} = \mp \frac{b^{2}}{\sqrt[]{a^{2} + b^{2}}}, & (4) \\ e = f = \sqrt[]{a^{2} + b^{2}} . \end{matrix}

(Ugyanez adódik persze

m = - 1

-ből is.) Mindezek szerint a keresett négyzet csúcsai a koordinátatengelyeken vannak, az az

O

centrumú kör metszi ki őket, melynek sugara egyenlő az ellipszis tengelyvégpontjai által meghatározott rombusz oldalával, vagy más szóval: a tengelyvégpontokbeli érintők által meghatározott téglalap átlójának felével (1. ábra).

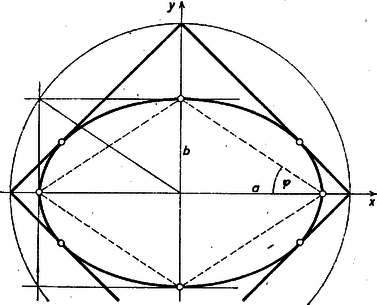1. ábra

Megjegyzések. 1. Tulajdonképpen többet végeztünk, mint amennyit a feladat megkívánt: egy körülírt négyzetet; mi pedig előbb megmutattuk, hogy csak egy négyzet van az ellipszis köré írható téglalapok közt, és azt szerkesztettük meg.
Mondhattuk volna ‐ mint a legtöbb dolgozat tette ‐: olyan megoldást keresünk, melyben a négyzet két szimmetriatengelye, az átlói, azonosak az ellipszis tengelyeivel. (Ekkor. persze még kérdéses, hogy van-e ilyen.) Itt tehát követelményként jelenik meg a (3) tengelymetszetek egyenlősége

\begin{matrix} e = \frac{a^{2}}{x_{1}} = \frac{b^{2}}{y_{1}} = \frac{a b}{\sqrt[]{a^{2} - x_{1}^{2}}}, x = \frac{a^{2}}{\sqrt[]{a^{2} + b^{2}}}, \frac{a^{2}}{x} = \sqrt[]{a^{2} + b^{2}}, \end{matrix}

és ezzel adódott, hogy van ilyen megoldás. (Kiadódik tükrözésekkel is) Ez önmagában elég csekély feladat, és nem tudjuk meg, hogy egy versenytárs nem állhat-e elő esetleg egy érdekesebb, mutatósabb eredménnyel.
2. Eljárhatunk úgy is a szerkesztésben, hogy először az ellipszis és a négyzet egyik oldala

E

érintkezési pontját szerkesztjük meg. Az I. síknegyedben (4) alapján

\begin{matrix} x_{1} = a \frac{a}{\sqrt[]{a^{2} + b^{2}}} = a cos φ, y_{1} = b \frac{b}{\sqrt[]{a^{2} + b^{2}}} = b sin φ, \end{matrix}

ahol

φ

a mondott rombuszoldal hajlásszöge az

x

tengelyhez. Fölmérjük a rombuszoldalra a kistengely végpontjából

a

-t, a nagytengely végpontjából

b

-t, az első végpont abszcisszában egyezik

E

-vel, a második pedig ordinátában (2. ábra).

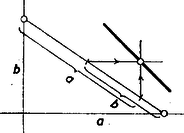2. ábra

3. Az oldalak irányát ismerve, 2 ‐ 2 pontjukat kaphatjuk az ellipszis következő tulajdonságának felhasználásával: a fókusznak bármely érintőn levő vetülete rajta van a főkörön (bizonyítását az olvasóra hagyjuk). Megszerkesztjük a két fókuszt, az ezeken át a tengelyekhez

45^{\circ}

-os szöggel hajló két-két egyenest, végül a főkört, ez metszi ki egyeneseinkből az említett pontokat.

Burda Magdolna (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)

II. megoldás. A négyzet átlóinak irányát határozzuk meg. Az a merőleges affinitás, amely az adott ellipszist a főkörébe viszi át, az ellipszisünk köré írt négyzetet a főkör köré írt paralelogrammába transzformálja, mert párhuzamos egyenesek megfelelői párhuzamosak. A kör köré írt paralelogramma rombusz, átlói merőlegesen metszik egymást a kör (egyszersmind az ellipszis) középpontjában. És mivel a rombusz átlói a négyzet átlóinak affin megfelelői, azért a négyzet átlói csak olyan (egymásra merőleges) egyenespáron lehetnek, amelyek affin megfelelői is merőlegesek.
Ilyen egyenespárt alkot az ellipszis két tengelye, és más ilyen nincs is. Ha ugyanis az

O

középpontból kiinduló

e, f

félegyenesek merőlegesek egymásra és a nagytengely egyik partján hozzá hegyes szöggel hajlanak, akkor az

\frac{a}{b} (> 1)

arányú affinitással kapott képeik közti szög hegyes szög lesz, mert az új és az eredeti hajlásszög tangensének aránya mindkét félegyenes esetében

\frac{a}{b}

, tehát a hajlásszögek nagyobbak, mint az eredetiek.
Ezzel beláttuk, hogy a keresett négyzet két átlója csak az ellipszis két tengelye lehet. Tovább a fentiek szerint haladhatunk.

^{$^{*}$}Az iskolai függvénytáblázat-gyűjtemény 385.4. képlete.