Kezdőlap


Feladat:	F.1854	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1973/december, 200 - 202. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Körülírt kör, Szinusztétel alkalmazása, Körérintési szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1972/december: F.1854

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Tekintsük először a különleges esetet. Ha a megrajzolt érintők párhuzamosak, akkor $A B$ a körnek átmérője, tehát az $A B C$ háromszögben $C$ -nél derékszög van, továbbá az $M$ pont ‐ szerkesztésénél fogva ‐ $C$ -nek a vetülete $A B$ -n (1. áb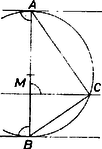ra).

1. ábra

Így az ismert mértani középarányos tétel szerint

\begin{matrix} \frac{A M}{M B} = \frac{A M \cdot A B}{B M \cdot B A} = \frac{A C^{2}}{B C^{2}} . \end{matrix}

2. Legyen a két érintő metszéspontja

P

, és a

P C

szelőnek a körrel való második metszéspontja

D

(különböző

C

-től, mert a szelő a két érintő közt halad).

C

és

D

szerepe a továbbiakban fölcserélhető, emiatt nincs szükség szétválasztani vizsgálatunkat két esetre,

P C

és

P D

nagyságviszonya szerint. Összekötve

D

-t

A

-val és

B

-vel és az érintőket meghosszabbítva, a 2. ábrán

A

-nál és

B

-nél négy-négy szöget jelöltünk meg egymástól megkülönböztető jelekkel,

C

-nél és

D

-nél pedig kettőt ‐ kettőt.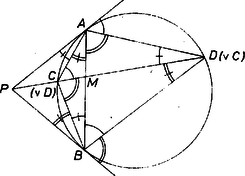

2. ábra

12

szög közül a kerületi szögek tételei alapján

3 - 3

(egyezően jelölt) szög egyenlő. Ezek alapján állítjuk párokba az alább felhasználandó hasonló háromszögeket.
Első lépésül a kérdéses

A M : M B

arányt kifejezzük az

A C B D

húrnégyszög oldalaival:

\begin{matrix} A M C ▵ \sim D M B ▵, emiatt: \frac{A M}{D M} = \frac{A C}{D B}, \\ D M A ▵ \sim B M C ▵, emiatt: \frac{D M}{B M} = \frac{D A}{B C}, \end{matrix}

és e két egyenlőség bal, valamint jobb oldalait összeszorozva

\begin{matrix} \frac{A M}{M B} = \frac{A C}{D B} \cdot \frac{D A}{B C} = \frac{A C}{B C} \cdot \frac{A D}{B D} . \end{matrix}

Második lépésül megmutatjuk, hogy

D

szerkesztése folytán itt a jobb oldal második tényezője egyenlő az elsővel, ezzel bebizonyítjuk az állítást. Valóban

\begin{matrix} P D A ▵ \sim P A C ▵, emiatt \frac{A D}{D P} = \frac{C A}{A P}, \\ P D B ▵ \sim P B C ▵, emiatt \frac{D P}{D B} = \frac{B P}{B C} . \end{matrix}

Végül ezeket összeszorozva és figyelembe véve

P A

és

P B

egyenlőségét:

\begin{matrix} \frac{A D}{B D} = \frac{A C}{B C}, \end{matrix}

amint állítottuk. ‐Megjegyezzük végül, hogy legutóbbi eredményünk ön-magában is érdekes, ha ti.

C D

átmegy az

A

‐és

B

-beli érintők közös pontján.

II. megoldás. A 3. ábra szögjelöléseivel a

P

létezése és a

P C < P M

nagyságviszony esetére a háromszög sinustételének ismételt alkalmazásával bizonyítjuk az állítást, figyelembe véve, hogy a

C

-nél a

P M

egyenes két oldalán keletkezett kiegészítő szögek sinusa egyenlő, és hogy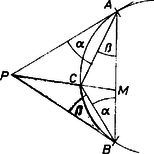

P A = P B

3. ábra

\begin{matrix} \frac{A M}{M B} = \frac{A M}{C M} \cdot \frac{C M}{M B} = \frac{sin A C M ∢}{sin β} \cdot \frac{sin α}{sin M C B ∢} = \frac{sin A C P ∢}{sin B P C ∢} \cdot \frac{sin α}{sin β} = \\ = \frac{\frac{A P}{P C} sin α}{\frac{B P}{P C} \cdot sin β} \cdot \frac{sin α}{sin β} = {(\frac{sin α}{sin β})}^{2} = {(\frac{A C}{B C})}^{2} . \end{matrix}

(A felhasznált háromszögek egymás után

A C M

és

B C M

, majd

A C P

és

B C P

, végül

A B C

Megjegyzések. 1. A két érintő párhuzamosságának esetét a II. megoldásban már figyelmen kívül hagytuk. Az állításnak ez a kiegészítése csak a teljesség kedvéért történt. Ugyanis

A

és

B

speciális kölcsönös helyzete esetében is van az

A B

szakaszon olyan

M

pont, melyre

A M : M B = {A C}^{2} : {B C}^{2}

, és erre az esetre mondja az állítás, hogy az

M C

egyenes ekkor is egyszerű kapcsolatba hozható az

A

és a

B

pontbeli érintővel.
2. Ajánljuk az érdeklődőknek, hozzák kapcsolatba feladatunkat az 1973. évi Arany Dániel tanulóversenyek haladó csoportbeli egyik feladatával: a háromszög egyik súlyvonalát tükrözve a vele közös csúcsból induló szögfelezőre, a tükörkép a szemközti oldalt olyan arányban osztja, mint a csúcsban összefutó oldalak négyzeteinek aránya. (A tükörképet röviden szimmediánnak szokás nevezni, mint a medián-súlyvonal szimmetrikusát.)