Kezdőlap


Feladat:	F.1850	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1973/április, 164 - 166. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Körök, Hossz, kerület, Koszinusztétel alkalmazása, Szöveges feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1972/november: F.1850

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Elég a $λ > 1$ értékekkel foglalkoznunk, mert ez ‐ ha kell ‐ a két torony sorrendjének fölcserélésével elérhető, ha pedig $λ = 1$ , akkor nyilvánvalóan megfelel az $A$ , $B$ talppontok közti szakasz $F$ felezőpontja, és más pont nem felel meg. (A mondott fölcserélés elérhető az $F$ körüli $180^{\circ}$ -os elfordítás útján is, és így az út önmagába megy át.)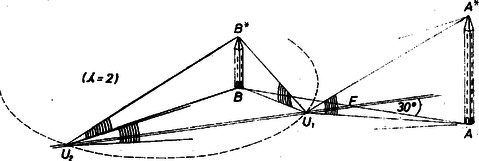

1. ábra

A tornyok csúcsát rendre

A^{*}

-gal,

B^{*}

-gal és az út egy megfelelő pontját

U

-val jelölve az

A^{*} U A

és

B^{*} U B

derékszögű háromszögek a látószögek egyenlősége alapján hasonlók (1. ábra), ezért

\begin{matrix} U A : U B = A A^{*} : B B^{*} = λ, U A > U B, \end{matrix}

ennélfogva

U F B ∢ = 30^{\circ}

U F A ∢ = 150^{\circ}

. Legyen még

A B / 2 = A F = a

és

F U = x

, ekkor az

U F A

U F B

háromszögekből a cosinustétel alkalmazásával

\begin{matrix} \frac{U A^{2}}{U B^{2}} = \frac{x^{2} + a^{2} + \sqrt[]{3} a x}{x^{2} + a^{2} - \sqrt[]{3} a x} = λ^{2}, \end{matrix}

és a szokásos lépésekkel

\begin{matrix} {(\frac{x}{a})}^{2} - \frac{\sqrt[]{3} (λ^{2} + 1)}{λ^{2} - 1} \cdot \frac{x}{a} + 1 = 0, & (1) \\ {(\frac{x}{a})}_{1,2} = \frac{\sqrt[]{3}}{2} \cdot \frac{λ^{2} + 1}{λ^{2} - 1} \pm \sqrt[]{\frac{3}{4} {(\frac{λ^{2} + 1}{λ^{2} - 1})}^{2} - 1}, & (2) \end{matrix}

hacsak a gyökjel alatt nemnegatív szám áll. Ezzel meghatároztuk a kívánt tulajdonságú pontoknak az úton elfoglalt helyzetét,

F A

egységekben mérve.
2. A megoldások száma

0

1

, illetőleg

2

aszerint, hogy a

D

diszkrimináns negatív,

0

, ill. pozitív. Ezt a föltételt kell úgy átalakítanunk, hogy közvetlenül

λ

értékéből adhassunk választ a kérdésre. Előrebocsátjuk, hogy a

\frac{λ^{2} + 1}{λ^{2} - 1}

hányados a

λ > 1

föltevés folytán pozitív, így a

D ⋚ 0

egyenlőtlenség

λ

-ra való megoldása esetszétválasztás nélkül halad:

\begin{matrix} \frac{3}{4} {(\frac{λ^{2} + 1}{λ^{2} - 1})}^{2} - 1 & ⋚ 0, \\ \frac{λ^{2} + 1}{λ^{2} - 1} = 1 + \frac{2}{λ^{2} - 1} & ⋚ \frac{2}{\sqrt[]{3}}, \\ \frac{1}{λ^{2} - 1} & ⋚ \frac{2 - \sqrt[]{3}}{2 \sqrt[]{3}} = \frac{1}{2 \sqrt[]{3} (2 + \sqrt[]{3})}, \\ λ^{2} - 1 & ⋛ 4 \sqrt[]{3} + 6, \\ λ^{2} & ⋛ 7 + 4 \sqrt[]{3} = {(2 + \sqrt[]{3})}^{2} . \end{matrix}

Ezek szerint

λ > 2 + \sqrt[]{3}

esetén nincs megoldás

U

-ra,

λ = 2 + \sqrt[]{3}

esetén egyetlen megoldás:

\begin{matrix} \frac{x}{a} = \frac{\sqrt[]{3}}{2} \cdot \frac{λ^{2} + 1}{λ^{2} - 1} = 1, \end{matrix}

1 < λ < 2 + \sqrt[]{3}

esetén pedig

2

megoldás van, és mindkettő pozitív, hiszen (1) együtthatói szerint összegük is, szorzatuk is pozitív.

II. megoldás. Ismeretes, hogy ‐ a fönti jelölésekkel ‐ a síknak az

U A : U B = λ (> 1)

föltételnek eleget tevő pontjai az

A

B

alappontokkal és a

λ

aránymutatóval meghatározott

k_{λ}

Apollóniosz-körön vannak. Ez szimmetrikus az

A B

egyenesre, az

A B

-n levő pontjai egy átmérőjét jelölik ki.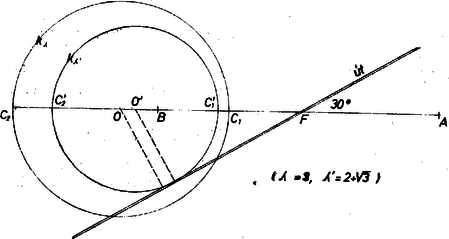

2. ábra

A B

szakaszon levő (belső)

C_{1}

osztópontra

C_{1} B = \frac{2 a}{λ + 1}

, a meghosszabbításon levő (külső)

C_{2}

-re

B C_{2} = \frac{2 a}{λ - 1}

(2. ábra), így az átmérő

C_{1} C_{2} = C_{1} B + B C_{2} = \frac{4 λ a}{λ^{2} - 1}

, az

O

középpont távolsága

F

-től

\begin{matrix} F O = F C_{1} + \frac{C_{1} C_{2}}{2} = F B - C_{1} B + \frac{2 λ a}{λ^{2} - 1} = \frac{a (λ^{2} + 1)}{λ^{2} - 1}, \end{matrix}

az úttól pedig

F O sin 30^{\circ} = F O / 2

. Mármost a kör és az út közös pontjainak száma aszerint

2

1

, ill.

0

, hogy ez a távolság kisebb, mint a kör sugara, ill. egyenlő vele, ill. nagyobb nála:

\begin{matrix} \frac{a (λ^{2} + 1)}{2 (λ^{2} - 1)} ⋚ \frac{2 a λ}{λ^{2} - 1}, \end{matrix}

azaz hogy

\begin{matrix} λ^{2} + 1 ⋚ 4 λ . \end{matrix}

Ebből ismét a fenti eredményt kapjuk.