Feladat:	F.1849	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bacsó G. ,  Bara Tamás ,  Bartha M. ,  Bezdek K. ,  Borbély A. ,  Burda Magdolna ,  Ernhöffer F. ,  Fazekas l. ,  Fóti P. ,  Fukker B. ,  Fürst A. ,  Hargitai B. ,  Hasenfratz Anna ,  Horváth Eszter ,  Horváth László ,  Horváth Ottó ,  Kiss Emil ,  Kobzos Katalin ,  Kollár J. ,  Kószó K. ,  Kovács S. ,  Lakner P. ,  Lux I. ,  Márkus J. ,  Nagyistók Katalin ,  Orosz Á. ,  Páles Zs. ,  Pócsi Gy. ,  Rapp F. ,  Schvarcz T. ,  Sliz M. ,  Szabó Gy. ,  Szabó Klára ,  Szelenszky G. ,  Szép Katalin ,  Sövér F. ,  Terlaky T. ,  Veres S. ,  Vörös Z.
Füzet:	1974/január, 7 - 10. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Trigonometriai azonosságok, Szögfelező egyenes, ( x + 1/x ) > = 2 ( x > 0 ), Feladat
Hivatkozás(ok):	Feladatok: 1972/november: F.1849

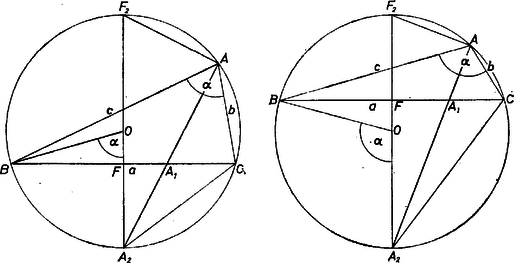
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle \frac{A{A}_1}{A{A}_2}+\frac{B{B}_1}{B{B}_2}+\frac{C{C}_1}{C{C}_2}\leqq \frac{9}{4}\mathrm{.}}\end{array}$ (1) I. megoldás. Az $A_2{A}_{1}C$ háromszög hasonló az $A_{2}CA$ háromszöghöz, mert $A_2$-nél levő szögük közös, továbbá $A_{1}C{A}_2\sphericalangle =BC{A}_2\sphericalangle =BA{A}_2\sphericalangle =CA{A}_2\sphericalangle$. A megfelelő oldalak arányából $\begin{array}{c}{\displaystyle A_1{A}_2=A_{2}C\frac{A_{1}C}{CA}\mathrm{,}{A}_{2}A=C{A}_2\frac{CA}{A_{1}C}\mathrm{,}}\end{array}$ és így (1) első tagja a háromszög oldalainak szokásos jelölésével a szögfelező osztásaránya alapján: $\begin{array}{c}{\displaystyle \frac{A{A}_1}{A{A}_2}=\frac{A{A}_2-A_1{A}_2}{A{A}_2}=1-{\left(\frac{A_{1}C}{CA}\right)}^2=1-{\left(\frac{\frac{ab}{b+c}}{b}\right)}^2=1-{\left(\frac{a}{b+c}\right)}^2\mathrm{.}}\end{array}$ Mivel a $B_1$ és $C_1$, valamint a $B_2$ és $C_2$ pontokat ugyanúgy kapjuk, mint $A_1$-et, illetve $A_2$-t, azért az $A$, $B$, $C$, valamint $a$, $b$, $c$ betűk ciklikus felcserélésével (1) további tagjait kifejezve, (1) helyett azt bizonyíthatjuk, hogy minden háromszögben $\begin{array}{c}{\displaystyle {\left(\frac{a}{b+c}\right)}^2+{\left(\frac{b}{c+a}\right)}^2+{\left(\frac{c}{a+b}\right)}^2\ge \frac{3}{4}\mathrm{.}}\end{array}$ A nyilvánvaló $\begin{array}{c}{\displaystyle {\left(u+v\right)}^2\le 2u^2+2v^2}\end{array}$ azonosságból $\begin{array}{c}{\displaystyle \frac{1}{{\left(u+v\right)}^2}\ge \frac{1}{2\left(u^2+v^2\right)}\mathrm{,}}\end{array}$ ennek alapján elég ezt bizonyítanunk: $\begin{array}{c}{\displaystyle \frac{a^2}{b^2+c^2}+\frac{b^2}{c^2+a^2}+\frac{c^2}{a^2+b^2}\ge \frac{3}{2}\mathrm{.}}\end{array}$ (2) Bevezetve az $\begin{array}{c}{\displaystyle x=b^2+c^2\mathrm{,}y=c^2+a^2\mathrm{,}z=a^2+b^2}\end{array}$ jelöléseket, a számlálók, majd (2) így alakulnak: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 2a^2=y+z-x\mathrm{,}2b^2=z+x-y\mathrm{,}2c^2=x+y-z\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{y+z-x}{x}+\frac{x+z-y}{y}+\frac{x+y-z}{z}\ge \mathrm{3,}}\hfill \\ \hfill {\displaystyle \left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)+\left(\frac{z}{x}+\frac{x}{z}\right)\ge \mathrm{6,}}\hfill \end{array}}$ ami nyilvánvaló az ismert $\begin{array}{c}{\displaystyle x+\frac{1}{x}\ge 2}\end{array}$ egyenlőtlenség alapján. Könnyű belátni, hogy egyenlőség mindenütt akkor és csak akkor áll, ha $a=b=c$.   Bara Tamás (Szeged, Ságvári E. Gyak. Gimn., IV. o. t.)   II. megoldás. A szögfelezés, a $BA{A}_2$ és $CA{A}_2$ kerületi szögek egyenlősége alapján a száraik közti $B{A}_2$, $C{A}_2$ ívek valamint húrok is egyenlők, ezért $A_2$ rajta van a $BC$ oldal felező merőlegesén. Jelöljük ennek a $BC$ oldalon levő pontját $F$-fel, a körön levő másik pontját $F_2$-vel.     Így $A_2{F}_{2}A$ és $A_2{A}_{1}F$ derékszögű háromszögek ‐ vagy pedig $F_2$ azonos $A$-val, $F$ az $A_1$-gyel ‐, ezért $A_1{A}_2\ge F{A}_2$ és $A{A}_2\ge F_2{A}_2$, tehát ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{A_1{A}_2}{A{A}_2}\ge \frac{F{A}_2}{F_2{A}_2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{A{A}_1}{A{A}_2}=1-\frac{A_1{A}_2}{A{A}_2}\le 1-\frac{F{A}_2}{F_2{A}_2}=\frac{F_{2}F}{F_2{A}_2}\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Mármost $F_{2}F=F_{2}O\pm OF$, aszerint véve az előjelet, hogy a $BAC\sphericalangle =BO{A}_2\sphericalangle$ hegyesszög-e vagy tompaszög. Ez a vagylagosság ismét egységgé válik, ha $OF$-et az $OB$ sugár vetületének tekintjük az $O$-tól $A_2$ felé irányított $F_2{A}_2$ átmérőre (a szögek szokásos jelölésével): $\begin{array}{c}{\displaystyle \frac{F_{2}F}{F_2{A}_2}=\frac{F_{2}O+OB\text{cos}\alpha }{2F_{2}O}=\frac{1}{2}+\frac{1}{2}\text{cos}\alpha \mathrm{,}}\end{array}$ tehát (1) első tagjára $\begin{array}{c}{\displaystyle \frac{A{A}_1}{A{A}_2}\le \frac{1}{2}+\frac{1}{2}\text{cos}\alpha \mathrm{.}}\end{array}$ (4) Meggondolásunk a betűk kellő cseréjével (1) második és harmadik tagjára is érvényes, ezért (1) bizonyítására elegendő igazolni a belőle (4)-nek és megfelelőinek behelyettesítésével adódó $\begin{array}{c}{\displaystyle \text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma \le \frac{3}{2}}\end{array}$ (5) egyenlőtlenséget. Itt ismert goniometrikus azonosságok alapján az első két tag összegére $\begin{array}{c}{\displaystyle 2\text{cos}\frac{\alpha +\beta }{2}\text{cos}\frac{\alpha -\beta }{2}\le 2\text{cos}\frac{\alpha +\beta }{2}=2\text{sin}\frac{\gamma }{2}\mathrm{,}}\end{array}$ (6) mert $\left(\alpha +\beta \right)/2<{90}^{\circ }$; a harmadik tag $1-2\text{sin}{}^2\gamma /2$, ezekkel pedig (5) jobb és bal oldalának különbsége nem kisebb, mint $\begin{array}{c}{\displaystyle \frac{1}{2}+2\text{sin}{}^2\frac{\gamma }{2}-2\text{sin}\frac{\gamma }{2}=2{\left(\text{sin}\frac{\gamma }{2}-\frac{1}{2}\right)}^2\ge 0.}\end{array}$ (7) Ezzel (5)-öt ‐ ami különben elég gyakran előforduló egyenlőtlenség a háromszög szögeire ‐ és vele a feladat állítását is bebizonyítottuk. (3)-ban, (4)-ben és (6)-ban ‐ mint említettük ‐ egyenlőség áll, ha $AB=AC$; ezért ha még $BC=AB$ is fennáll, vagyis ha az $ABC$ háromszög egyenlő oldalú akkor (5) és (7) két oldala is egyenlő. Ebben az esetben, de csakis ekkor, egyenlőség áll (1)-ben is. Valóban, szabályos háromszög esetében (1) bal oldalának mindhárom tagja $3/4$.   Megjegyzés. Meg lehet mutatni, hogy $A{A}_1=f_a$ jelöléssel $\begin{array}{c}{\displaystyle \frac{A{A}_1}{A{A}_2}=\frac{f_a^2}{bc}\mathrm{,}}\end{array}$ ezzel (1) így alakul: $\begin{array}{c}{\displaystyle \frac{f_a^2}{bc}+\frac{f_b^2}{ca}+\frac{f_c^2}{ab}\le \frac{9}{4}\mathrm{.}}\end{array}$ Az 1799. feladatban${}^{*}$ viszont ezt bizonyítottuk: $\begin{array}{c}{\displaystyle \frac{s_a^2}{bc}+\frac{s_b^2}{ca}+\frac{s_c^2}{ab}\ge \frac{9}{4}\mathrm{,}}\end{array}$ ahol a számlálókban a súlyvonalak hossza áll. Végül a magasságokra $\begin{array}{c}{\displaystyle m_a\le f_a\left(\le s_a\right)\mathrm{,}}\end{array}$ tehát ezekre méginkább $\begin{array}{c}{\displaystyle \frac{m_a^2}{bc}+\frac{m_b^2}{ca}+\frac{m_c^2}{ab}\le \frac{9}{4}\mathrm{.}}\end{array}$ ${}^{*}$Lásd K.M. L. (1973) 118. old.