Kezdőlap


Feladat:	F.1844	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1973/március, 106 - 108. oldal		PDF \| MathML
Témakör(ök):	Nevező gyöktelenítése, Merőleges affinitás, Egyenesek egyenlete, Ellipszis egyenlete, Hiperbola egyenlete, Kúpszeletek érintői, Koordináta-geometria, Feladat
Hivatkozás(ok):	Feladatok: 1972/október: F.1844

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Két görbéről akkor mondjuk, hogy érintik egymást, ha van közös pontjuk és ebben közös az érintőjük, vagyis érintőjük (változó) iránytangense a közös pontban egyenlő.
Görbéink közös pontjainak $x_{k}$ abszcisszájára a két egyenletből $y$ kiküszöbölésével a következő adódik:

\begin{matrix} \frac{x_{k}^{2}}{a^{2}} + \frac{1}{b^{2} x_{k}^{2}} = 1, \\ x_{k}^{4} - a^{2} x_{k}^{2} + \frac{a^{2}}{b^{2}} = 0 \end{matrix}

(szabad szorozni

x_{k}^{2}

-nel, hiszen

x_{k} \neq 0

, mert hiperbolánknak nincs pontja az

x = 0

abszcisszán). Innen

\begin{matrix} x_{k}^{2} = \frac{a^{2}}{2} \pm g, x_{k} = \pm \sqrt[]{\frac{a^{2}}{2} \pm g}, \end{matrix}

ahol

\begin{matrix} g = \sqrt[]{\frac{a^{4}}{4} - \frac{a^{2}}{b^{2}}} . \end{matrix}

(1)

Mindkét görbénk centrálisan szimmetrikus az origóra, tehát érintkezési pontjaik is páronként egymás tükörképei, ezért elég az érintők iránytangensének egyenlőségét a pozitív abszcisszájú közös pontokban biztosítani.

x_{k} > 0

alapján a hiperbola révén

y > 0

, ezért az ellipszis egyenletéből a felső íven levő pont ordinátáját fejezzük ki a deriválás céljára:

\begin{matrix} y = \frac{b}{a} \sqrt[]{a^{2} - x^{2}}, y' = - \frac{b}{a} \cdot \frac{x}{\sqrt[]{a^{2} - x^{2}}} . \end{matrix}

Eszerint a közös pontban,

x = x_{k}

és a kapott kifejezések helyettesítésével az iránytangens [a nevező gyöktelenítése után és (1) figyelembevételével]

\begin{matrix} - \frac{b}{a} \cdot \frac{\sqrt[]{\frac{a^{2}}{2} \pm g}}{\sqrt[]{\frac{a^{2}}{2} \mp g}} = - \frac{b}{a} \cdot \frac{\sqrt[]{{(\frac{a^{2}}{2})}^{2} - g^{2}}}{\frac{a^{2}}{2} \mp g} = - \frac{1}{\frac{a^{2} \mp g}{2}} . \end{matrix}

A hiperbola érintőjének iránytangense hasonlóan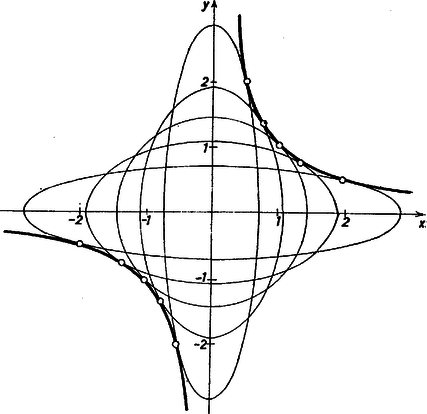

\begin{matrix} y = \frac{1}{x}, y' = - \frac{1}{x^{2}}, - \frac{1}{x_{k}^{2}} = - \frac{1}{\frac{a^{2}}{2} \pm g}, \end{matrix}

és ezt az előbbivel egybevetve látjuk, hogy közös pontjukban csak akkor lehet az érintő is közös, ha

\begin{matrix} g = 0, azaz \frac{a^{4}}{4} - \frac{a^{2}}{b^{2}} = 0, a b = 2 \end{matrix}

(hiszen

a

és

b

természetesen pozitívok).

Ezzel megkaptuk

a

és

b

keresett összefüggését. E föltétel teljesülése esetén 2 közös pontja van görbéinknek:

(a / \sqrt[]{2}, b / \sqrt[]{2})

és

(- a / \sqrt[]{2}, - b / \sqrt[]{2})

, de az ellipszis nincs egyértelműen meghatározva, az

a

paramétertől függő

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{a^{2} y^{2}}{4} = 1 \end{matrix}

egyenletű ellipszissereg minden egyede érinti a rögzített

y = 1 / x

hiperbolát a paraméterrel megadott érintési pontban.

II. megoldás. Ismeretes a tankönyvből,¹ hogy az

y = 1 / x

hiperbolának az

(x_{0}; 1 / x_{0})

pontbeli érintője a

(2 x_{0}; 0)

pontban metszi az

x

tengelyt. Továbbá, hogy ellipszisünk az

x^{2} + y^{2} = a^{2}

kör képe egy olyan merőleges affinitásban, melynek tengelye az

x

tengely.²
Be lehet bizonyítani, hogy a kör és az ellipszis egy megfelelő pontpárjában vett érintőik is egymás affin képei, és így egymást az affinitás tengelyén metszik. Ezek szerint az ellipszis és hiperbola közös pontjának

x_{k}

abszcisszáját az jellemzi, hogy az

x^{2} + y^{2} = a^{2}

körhöz az

x_{k}

abszcisszájú pontjában húzott érintő a

(2 x_{k}; 0)

pontban metszi az

x

tengelyt. Mármost az érintő egyenlete³

\begin{matrix} x_{k} \cdot x + \sqrt[]{a^{2} - x_{k}^{2}} \cdot y = a^{2}, \end{matrix}

s mivel ezt a mondott pont koordinátái kielégítik,

2 x_{k}^{2} = a^{2}

x_{k}^{2} = a^{2} / 2

. Így a közös pont ordinátája a hiperbola révén

\begin{matrix} y_{k} = \frac{1}{x_{k}} = \frac{\sqrt[]{2}}{a}, \end{matrix}

az ellipszis révén

\begin{matrix} y_{k} = \frac{b}{a} \cdot \sqrt[]{a^{2} - \frac{a^{2}}{2}} = \frac{b}{\sqrt[]{2}}, \end{matrix}

és e kettő egyenlőségéből

a b = 2

Megjegyzés. Görbék érintkezését a tankönyv nem definiálja. A megoldók legtöbbje úgy jutott célhoz, hogy az ellipszis és hiperbola egyenletéből az egyik koordinátát kiküszöbölve, a másikra kapott egyenletre írta elő, hogy többszörös gyöke legyen, diszkriminánsa legyen 0, ezáltal legalább két közös pont egybeesik. A korábbi tankönyv így vizsgálta parabola és egyenes érintkezésének feltételét.
Elfogadtuk az ilyen megoldásokat, de ilyet nem közöltünk, mert ez az elv nem használható, ha nem mindkét görbe egyenlete algebrai egyenlet és akkor sem, ha magasabb fokú. Az itt fölhasznált eszközök viszont ismeretesek a tananyagból, görbe és egyenes (elsőfokú görbe) érintkezését éppen a fenti módon definiálja a tankönyv.⁴

¹Czapáry E.‐Horvay K.‐Pálmay L.: Matematika a gimn. és szakközépisk. III. o. számára. Tankönyvkiadó, Budapest. 1968. 318 old.

²Ugyanott, 168. old.

³Ugyanott, a 198. oldalon, a 133. feladat megoldásának mintájára.

⁴Ugyanott, 294. old.