Kezdőlap


Feladat:	F.1843	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bara T. , Bezdek K. , Csuka G. , Diósi L. , Dombovári T. , Fejér Sz. , Hargitai B. , Horváth Eszter , Kópházi J. , Kovács F. , Páles Zs. , Rövid K. , Simányi N. , Sőnfeld J. , Stettner Eleonóra , Szabó György , Szabó Klára , Terlaky T.
Füzet:	1974/március, 97 - 99. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Súlyvonal, Szögfelező egyenes, Körülírt kör, Egyenesek egyenlete, Osztópontok koordinátái, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1972/október: F.1843

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Helyezzünk koordinátarendszert az alakzatra, legyen az origója $A_{0}$ , $x$ tengelye a $B C$ egyenes, a csúcsok koordinátái $B (- a / 2, 0)$ , $C 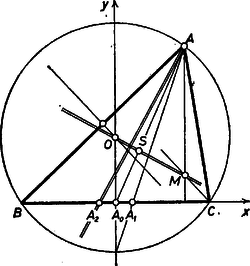(a / 2, 0)$ , $A (d, m_{a})$ (1 ábra.).

1. ábra

A B = A C

esetet ‐ ill. a szokásos jelöléssel

c = b

‐ eleve kizárjuk, mert ekkor a föltevés szerint

a = b = c

, a háromszög egyenlő oldalú, az állításbeli

S O

egyenes határozatlan, az állítás tárgytalan.
Legyen

A_{1}

abszcisszája

e

, erre a szögfelező osztási aránya alapján

\begin{matrix} A B : A C = A_{1} B : A_{1} C, \end{matrix}

\begin{matrix} c : b = (e + \frac{a}{2}) : (\frac{a}{2} - e) \\ e = \frac{a (c - b)}{2 (b + c)}, (\neq 0) \end{matrix}

és mivel az értelmezés szerint

A_{2} (- e, 0)

, ezért az

A A_{2}

egyenes iránytangense

\begin{matrix} m_{1} = \frac{m_{a}}{d + e} = \frac{2 m_{a} (b + c)}{2 d (b + c) + a (c - b)} . \end{matrix}

(1)

A súlypont koordinátái:

S (d / 3, m_{a} / 3)

.
A körülírt kör

O

középpontját az

A B

szakasz felező merőlegese metszi ki

B C

felező merőlegeséből, az

y

tengelyből. Az

A B

szakasz felezőpontja és iránytangense

\begin{matrix} (\frac{d}{2} - \frac{a}{4}, \frac{m_{a}}{2}), \frac{m_{a}}{d + \frac{a}{2}} = \frac{2 m_{a}}{2 d + a}, \end{matrix}

így felező merőlegesének egyenlete, majd abból

x = 0

helyettesítéssel

O

-nak

y_{0}

ordinátája

\begin{matrix} y & - \frac{m_{a}}{2} = - \frac{2 d + a}{2 m_{a}} (x - \frac{d}{2} + \frac{a}{4}), \\ y_{0} = \frac{m_{a}}{2} & - \frac{2 d + a}{2 m_{a}} (\frac{a}{4} - \frac{d}{2}) = \frac{4 m_{a}^{2} - a^{2} + 4 d^{2}}{8 m_{a}} . \end{matrix}

Ezekkel az

S O

egyenes iránytangense (mivel

d \neq 0

)

\begin{matrix} m_{2} = \frac{y_{0} - \frac{m_{a}}{3}}{- \frac{d}{3}} = - \frac{12 d^{2} + 4 m_{a}^{2} - 3 a^{2}}{8 d m_{a}} . \end{matrix}

Az állítás szerint az

a^{2} = b c

föltevés mellett

m_{1}

és

m_{2}

egymás negatív reciprokai. Ennek igazolására szorozzuk számlálóját és nevezőjét

(c - b)

-vel:

\begin{matrix} m_{1} = \frac{2 m_{a} (c^{2} - b^{2})}{2 d (c^{2} - b^{2}) + a {(c - b)}^{2}}, \end{matrix}

(2)

és fejezzük ki

b

-t,

c

-t a koordinátákkal:

\begin{matrix} b^{2} = {(d - \frac{a}{2})}^{2} + m_{a}^{2}, c^{2} = {(d + \frac{a}{2})}^{2} + m_{a}^{2} . \end{matrix}

Innen, a

b c = a^{2}

föltevést is fölhasználva

\begin{matrix} c^{2} - b^{2} = 2 a d, \\ {(c - b)}^{2} = c^{2} + b^{2} - 2 a^{2} = 2 d^{2} + 2 m_{a}^{2} - \frac{3}{2} a^{2} . \end{matrix}

Ezekkel (2) így alakul:

\begin{matrix} \frac{4 a d m_{a}}{4 a d^{2} + a (2 d^{2} + 2 m_{a}^{2} - \frac{3}{2} a^{2})} = \frac{8 d m_{a}}{12 d^{2} + 4 m_{a}^{2} - 3 a^{2}}, \end{matrix}

és ez valóban negatív reciproka

m_{2}

-nek. Ezzel az állítást bebizonyítottuk minden olyan esetre, ha

A B \neq A C

. Ismeretes ugyanis, hogy

S

csak az egyenlő oldalú háromszögben esik egybe

O

-val, másrészt

c > b

mellett

d > 0

e > 0

, a felhasznált

d + e

2 d + a

c - b

nevezők, ill. szorzó mindegyike pozitív.
Stettner Eleonóra (Kaposvár, Táncsics M. Gimn., IV. o. t.)

II. megoldás. Azok számára, akik ismerik a vektorok skaláris szorzatát, leírunk egy második megoldást is. Válasszuk origónak az

A

csúcsot,

B

és

C

helyvektorát jelöljük rendre

b

-vel,

c

-vel, e vektorok hosszát

λ

-val és

μ

-vel (2. áb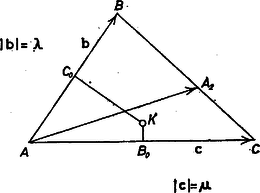ra).

2. ábra

Akkor

A_{2}

helyvektora

\begin{matrix} {\vec{A A}}_{2} = \frac{λ b + μ c}{λ + μ}, \end{matrix}

a háromszög

S

súlypontjának a helyvektora pedig

\begin{matrix} \vec{A S} = \frac{b + c}{3} . \end{matrix}

A körülírt kör

K

középpontjának a helyvektora

\begin{matrix} \vec{A K} = y b + z c \end{matrix}

olyan

y

és

z

skaláris mennyiségekkel, amelyekre

K C_{0} ⊥ A B

és

K B_{0} ⊥ A C

, azaz amelyekre teljesül

\begin{matrix} [(y - \frac{1}{2}) b + z c] b = 0, [y b + (z - \frac{1}{2}) c] c = 0. \end{matrix}

(4)

Azt kell megmutatnunk, hogy

S K ⊥ A A_{2}

, azaz

\begin{matrix} [(y - \frac{1}{3}) b + (z - \frac{1}{3}) c] (λ b + μ c) = 0. \end{matrix}

Szorozzuk meg (3)-et

λ

-val, (4)-t

μ

-vel, és a kapott egyenleteket adjuk össze:

\begin{matrix} (y b + z c) (λ b + μ c) = \frac{λ^{3} + μ^{3}}{2} . \end{matrix}

Ennek alapján elég megmutatni, hogy

\begin{matrix} \frac{1}{3} (b + c) (λ b + μ c) = \frac{1}{2} (λ^{3} + μ^{3}), \\ 2 (λ^{3} + μ^{3}) + 2 (λ + μ) bc = 3 (λ^{3} + μ^{3}), \\ 2 bc = λ^{2} + μ^{2} - λ μ . \end{matrix}

Jelöljük

B C

hosszát

h

-val, akkor

\begin{matrix} 2 bc = λ^{2} + μ^{2} - {(b - c)}^{2} = λ^{2} + μ^{2} - h^{2}, \end{matrix}

tehát azt kell megmutatnunk, hogy

h^{2} = λ μ

ami viszont épp a feladatunk első feltétele; a bizonyítást befejeztük.