Kezdőlap


Feladat:	F.1842	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1973/május, 203 - 204. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Háromszögek nevezetes tételei, Háromszög nevezetes vonalai, Körök, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1972/október: F.1842

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög csúcsait $A$ , $B$ , $C$ betűvel, és legyen $A B = d + e + f$ úgy, hogy részei $A D = d$ , $D E = e$ , $E B = f$ , továbbá legyen $C A = b$ , $C D = g$ , $C E = h$ , $C B = a$ és $A C B ∢ = γ$ , ekkor a föltevés szerint 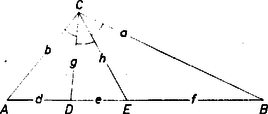$A C D ∢ = D C E ∢ = E C B ∢ = \frac{γ}{3}$ .

Fejezzük ki az

A C E

háromszög területét egyrészt

C A

C E

oldalaival és az

A C E

szöggel, másrészt az

A C D

és

D C E

háromszögek hasonlóan kifejezett területeinek összegeként:

\begin{matrix} \frac{1}{2} b h sin \frac{2 γ}{3} = b h sin \frac{γ}{3} cos \frac{γ}{3} = \frac{1}{2} (b g + g h) sin \frac{γ}{3} . \end{matrix}

Innen, mivel

γ > 0^{\circ}, sin (γ / 3) \neq 0

\begin{matrix} cos = \frac{γ}{3} = \frac{g (b + h)}{2 b h} . \end{matrix}

(1)

Betűzzük át eredményünket a

D C B

háromszögre, majd szorozzuk meg az új kifejezést (1)-gyel:

\begin{matrix} cos \frac{γ}{3} = \frac{h (g + a)}{2 g a}, \\ cos^{2} \frac{γ}{3} = \frac{(b + h) (g + a)}{4 b a} = \frac{1}{4} (1 + \frac{h}{b}) (\frac{g}{a} + 1) = & (2) \\ = \frac{1}{4} (1 + \frac{e}{d}) (\frac{e}{f} + 1) = \frac{(d + e) (e + f)}{4 d f} \end{matrix}

Felhasználtuk a továbbalakításban, hogy

C D

felezi az

A C E

szöget és

C E

felezi a

D C B

szöget, ennélfogva az ismert tétel szerint

\begin{matrix} \frac{C E}{C A} = \frac{D E}{D A} és \frac{C D}{C B} = \frac{E D}{E B}, \end{matrix}

így

γ

-t kifejeztük a

d, e, f

szakaszokkal
A számpéldákban rendre

\begin{matrix} cos^{2} \frac{γ}{3} = \frac{3}{4}, \frac{19^{2}}{4 \cdot 11^{2}}, 0, 7 \end{matrix}

adódik, s mivel

γ / 3

mindenesetre hegyesszög, cosinusa pozitív, azért rendre

\begin{matrix} cos \frac{γ}{3} = \frac{\sqrt[]{3}}{2}, \frac{19}{22}, 0, 8367, \\ cos γ = (4 cos^{2} \frac{γ}{3} - 3) cos \frac{γ}{3} = 0, - \frac{19}{11^{3}}, - 0, 1673, \\ γ = 90^{\circ}, 90^{\circ} 49', 99^{\circ} 38' . \end{matrix}

Megjegyzések. Az (1)-ben tulajdonképpen a

b, h

oldalakkal és a köztük levő szög

g

felezőjével meghatározott háromszög megfelezett szögét határoztuk meg, ami önmagában is érdekes eredmény.
2. Megkaphatjuk (2)-t abból is, hogy az

A B C

háromszög területe egyenlő az

A D C

D E C

és

E B C

háromszögek területének összegével, ha alkalmazzuk a sin

γ

-t a sin

(γ / 3)

-mal kifejező azonosságot:

\begin{matrix} (2 t =) a b \end{matrix}