Kezdőlap


Feladat:	F.1836	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Besenyei Lajos , Bogsch Imre , Bugyi Márta
Füzet:	1973/március, 103 - 105. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Trigonometrikus egyenlőtlenségek, Trigonometriai azonosságok, Egyenlő szárú háromszögek geometriája, Körök, Négyszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1972/szeptember: F.1836

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az $O$ csúcsú, $x$ nagyságú szög szárainak az $O$ körüli, egységnyi sugarú $k$ körrel közös pontját $A$ -val, ill. $B$ -vel, és messe egymást $k$ -nak $A$ -beli és $B$ -beli érintője $C$ -ben. Ekkor $O C$ felezi a szöget, és azt kell bizonyítanunk, hogy az $A C$ érintőszakasz kisebb, mint $k$ -nak (rövidebbik) $A B$ í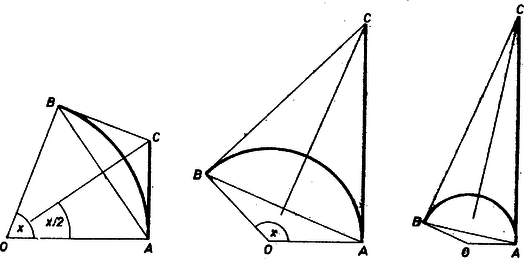ve.

Elég azt belátnunk, hogy

A C

‐ és a vele egyenlő

B C

‐ még az

A B

húrnál is rövidebb. E három szakasz az

A B C

egyenlő szárú háromszöget alkotja, így a velük szemben fekvő szögekre az

\begin{matrix} A B C ∢ = B A C ∢ < A C B ∢ \end{matrix}

(2)

egyenlőtlenség egyenértékű állításunkkal.
Mármost az

O A C B

négyszögből nyilvánvalóan

A C B ∢ = π - x

, és mint merőleges szárú hegyes szögek a (2)-beli első szög egyenlő

B O C ∢ = \frac{x}{2}

-vel, tehát (2) teljesül, amíg

\begin{matrix} \frac{x}{2} < π - x, azaz x < \frac{2}{3} π . \end{matrix}

Azt kaptuk tehát, hogy a

tg (x / 2) < x

egyenlőtlenség valamivel tágabb feltétel mellett is érvényes, mint amely mellett a feladat a bizonyítást követeli.

Bugyi Márta (Csongrád, Batsányi J. Gimn., IV. o. t.)

Megjegyzések. 1. A (2)-ben megengedhettük volna a

B A C

és

A C B

szögek egyenlőségét is, hiszen határozottan

\hat{A B} > \bar{A B}

. Egyébként könnyű látni a táblázatokból, hogy a

tg (x / 2) = x

egyenlőség közelítőleg

x = 2, 33 (= 133, 5^{\circ})

-nál következik be.
2. Mivel

A B = 2 sin (x / 2)

, bizonyításunkat így is mondhatjuk:

\begin{matrix} tg \frac{x}{2} = \frac{sin \frac{x}{2}}{cos \frac{x}{2}} < 2 sin \frac{x}{2} \end{matrix}

mindaddig teljesül, amíg

\begin{matrix} x > 0 és cos \frac{x}{2} > \frac{1}{2}, \end{matrix}

azaz

\begin{matrix} 0 < \frac{x}{2} < \frac{π}{3} . \end{matrix}

Besenyei Lajos (Eger, Gárdonyi G. Gimn., IV. o. t.)

II. megoldás. A feladat föltétele alapján

cos x ≧ 0

, így ismert azonosságot és egyenlőtlenségeket alkalmazva

\begin{matrix} tg \frac{x}{2} = \frac{sin x}{1 + cos x} ≦ sin x < x . \end{matrix}

A második lépésben alkalmazott becslés miatt itt nem olvashatjuk ki az állítás érvényességének kiterjesztését.

III. megoldás. Vizsgáljuk az

f (x) = x - tg \frac{x}{2}

függvény változását a

(0, \frac{π}{2})

intervallumban. A függvény deriváltja

\begin{matrix} f' (x) = 1 - \frac{1}{2 cos^{2} \frac{x}{2}}, \end{matrix}

pozitív az intervallum belsejében, tehát

f

szigorúan monoton növekedő. Mivel

f (0) = 0

, másrészt

f

az intervallum jobb végpontjában is folytonos, azért

\begin{matrix} f (x) > 0, ha 0 < x ≦ \frac{π}{2} . \end{matrix}

Ezzel bebizonyítottuk az állítást.

Bogsch Imre (Budapest, Eötvös J. Gimn., IV. o. t.)