Kezdőlap


Feladat:	F.1825	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1974/május, 193 - 194. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Trigonometriai azonosságok, Egyenes körkúpok, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1972/április: F.1825

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kúp csúcsa $C$ , alapkörének középpontja $O$ , a nagyobb nyílásszögű kúp kérdéses alkotói $C P_{2}$ és $C Q_{2}$ , továbbá az $O P_{2}$ , $O Q_{2}$ sugaraknak a kisebb nyílásszögű kúp alapkörén levő pontjai 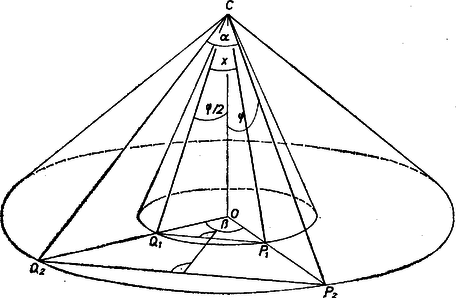$P_{1}$ , ill. $Q_{1}$ .

Ekkor egyrészt a

P_{2} C O ∢ = φ

és

P_{1} C O ∢ = φ / 2

félnyílásszögeket, másrészt a

C P_{1}

C Q_{1}

alkotók közti

P_{1} C Q_{1} = x

szöget kell meghatároznunk az adott

P_{2} C Q_{2} ∢ = α

-ból,

P_{2} C Q_{2} ∢ = P_{1} C Q_{1} ∢ = β

-ból.
Felhasználjuk, hogy

C P_{2} O

derékszögű háromszög,

C P_{2} Q_{2}

és

O P_{2} Q_{2}

, valamint

C P_{1} Q_{1}

és

O P_{1} Q_{1}

pedig egyenlő szárú háromszögek. A nagyobbik nyílásszögre

\begin{matrix} sin φ = \frac{O P_{2}}{C P_{2}} = \frac{P_{2} Q_{2} : (2 sin β / 2)}{P_{2} Q_{2} : (2 sin α / 2)} = \frac{sin α / 2}{sin β / 2}, \end{matrix}

(1)

és ezzel ‐ numerikusan megadott

α

β

szögek mellett ‐ a

φ / 2

kisebbik nyílásszöget is meghatározottnak tekinthetjük.
Eredményünk átvihető a belső kúpra úgy, hogy

φ

helyett

φ / 2

-t és

α

helyett

x

-et írunk:

\begin{matrix} sin \frac{φ}{2} = \frac{sin x / 2}{sin β / 2,} \end{matrix}

és innen az új alkotók közti, keresett szögre

\begin{matrix} sin \frac{x}{2} = sin \frac{β}{2} sin \frac{φ}{2} . \end{matrix}

(2)

Mivel valóságos kúpban az alkotó (

C P_{2}

C P_{1}

) nagyobb az alapkör sugaránál, azért a

C P_{i} Q_{i}

és

O P_{i} Q_{i}

(

i = 1, 2

) háromszögekben

C

-nél kisebb szög van, mint

O

-nál, tehát

α < β

, illetve

x < β

. Így, ha az adatokra

0^{\circ} < α < β < 180^{\circ}

, akkor (1) és (2) jobb oldala

0

és

1

közti szám, feladatunk egyértelműen megoldható.

Megjegyzés. Tetszetősebb, ha ismeretleneinket egyik alkalmas szögfüggvényük révén az (eredeti) adatok valamelyik szögfüggvényével fejezzük ki. Ehhez (1) alapján

\begin{matrix} cos φ = \sqrt[]{1 - sin^{2} φ} = \sqrt[]{1 - \frac{sin^{2} α / 2}{sin^{2} β / 2}} = \sqrt[]{\frac{cos α - cos β}{1 - cos β}}, \end{matrix}

és így a kisebbik nyílásszög közvetlenül

\begin{matrix} sin \frac{φ}{2} = \sqrt[]{\frac{1}{2} - \frac{1}{2} \sqrt[]{\frac{cos α - cos β}{1 - cos β}}}, \end{matrix}

ebből pedig (2) alapján

\begin{matrix} cos x = \frac{1}{2} (1 + cos β + \sqrt[]{(1 - cos β) (cos α - cos β)}) . \end{matrix}

A kisebbik nyílásszög még másképpen

\begin{matrix} tg \frac{φ}{2} = \frac{\sqrt[]{1 - cos β} - \sqrt[]{cos α - cos β}}{\sqrt[]{1 - cos α}} . \end{matrix}

Ezek igazolását az érdeklődő olvasóra hagyjuk.