| Feladat: | F.1824 | Korcsoport: 18- | Nehézségi fok: átlagos |
| Füzet: | 1975/november, 108 - 109. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Középpontos és egyéb hasonlósági transzformációk, Háromszögek nevezetes tételei, Számsorok, Mértani sorozat, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1972/április: F.1824 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük a , háromszögek arányú beírt háromszögeit -gal, illetve -sal (olvasd: há fölül vonás). Megmutatjuk, hogy a -nak arányú beírt háromszöge, és -ból az centrumú 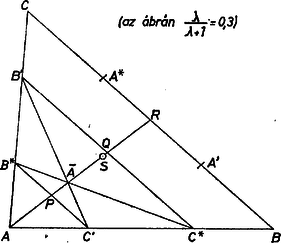 Mivel
Hasonlóan láthatók be a másik két csúcsára vonatkozó állításaink is, előrebocsátott megjegyzésünk bizonyítását ezzel befejeztük. A most bizonyított állítás szerint a -ből arányú centrális hasonlósággal kapható meg, tehát kerülete kerületének -szorosa. Eszerint a háromszögek kerületei mértani sorozatot alkotnak, amelyben az első tag , és a szomszédos elemek hányadosa , és . Ismeretes, hogy ebben az ( elemű) sorozatban az elemek összege , tehát a háromszögek kerületeinek összege, ha minden határon túl nő, Láttuk már, hogy egy háromszög arányú beírt háromszögének arányú beírt háromszöge megegyezik a háromszög arányú beírt háromszögének arányú beírt háromszögével. Emiatt a háromszögek kerületei is mértani sorozatot alkotnak, amelyben a szomszédos elemek hányadosa szintén . A feladat b) állítása tehát következik abból a tényből, hogy az azonos hányadosú (végtelen) mértani sorok összegei úgy aránylanak egymáshoz, mint e sorok első tagjai. |