Kezdőlap


Feladat:	F.1823	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Lakner Péter
Füzet:	1972/december, 211 - 214. oldal		PDF \| MathML
Témakör(ök):	Differenciálszámítás, Ponthalmazok, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1972/április: F.1823

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Görbénk centrálisan szimmetrikus az origóra, egy ( $x$ , $y$ ) pontjával együtt ennek ( $- x$ , $- y$ ) tükörképe is rajta van a görbén, hiszen erre teljesül $(- y) = {(- x)}^{3} - (- x)$ . Eszerint a görbe minden egyes érintőjének az origóra való tükörképe is érinti a görbét, a koordináta‐rendszer egy $P_{0} (x_{0}, y_{0})$ pontján át ugyanannyi érintője megy át a görbének, mint a $P'_{0}$ ( $- x_{0}$ , $- y_{0})$ ponton át. Elég tehát az $x_{0} ≧ 0$ előírással az $y$ tengelytől jobbra eső félsíkra és magára e tengelyre szorítkoznunk a vizsgálatban, a kapott eredmények tükrözéssel a sík minden pontjára megadják a választ.
$P_{0}$ -on az adott görbe $t$ abszcisszájú $(t, t^{3} - t)$ pontjához húzott $e$ érintő akkor és csak akkor megy át, ha $P_{0}$ koordinátái kielégítik $e$ egyenletét :

\begin{matrix} y_{0} - (t^{3} - t) = (3 t^{2} - 1) (x_{0} - t) \end{matrix}

(az iránytényező a görbénkhez tartozó

f (x) = x^{3} - x

függvény

f' (x) = 3 x^{2} - 1

deriváltjának értéke a

t

helyen), eszerint a megfelelő

t

értékeket mint az innen átrendezéssel adódó

\begin{matrix} φ (t) = 2 t^{3} - 3 x_{0} t^{2} + (x_{0} + y_{0}) = 0 \end{matrix}

(1)

egyenlet valós gyökeit kaphatnánk meg.

Feladatunk kérdése szempontjából azonban elég azt tudnunk, hogy hány valós gyöke van (1)-nek adott

P_{0}

esetében. Erre választ kapunk a

φ (t)

függvény menetének, görbéje fordulópontjainak vizsgálata alapján. (

φ (t)

görbéjét egy

t

u

koordináta‐rendszerben gondoljuk ábrázolva, de ez azonos is lehet az eredetivel.) Deriváltja eltűnik, ha

\begin{matrix} φ' (t) = 6 t^{2} - 6 x_{0} t = 6 t (t - x_{0}) = 0, \end{matrix}

azaz a

t = 0

és a

t = x_{0}

(≧ 0)

helyen.
Legyen egyelőre

x_{0} > 0

. Ekkor

φ (t)

-nek két különböző (valós) helyen van szélső értéke, görbéjének két fordulópontja

\begin{matrix} F_{1} (0, x_{0} + y_{0}) és F_{2} (x_{0}, x_{0} + y_{0} - x_{0}^{3}), \end{matrix}

és mivel

F_{2}

ordinátája kisebb, azért

F_{1}

φ (t)

maximumát,

F_{2}

a minimumát ábrázolja. A

φ (t)

görbe

t < 0

esetén emelkedik,

0 < t < x_{0}

esetén süllyed,

t > x_{0}

esetén ismét emelkedik.

α

) Ha mármost

F_{1}

és

F_{2}

ugyanazon az oldalán van a

t

tengelynek, más szóval

F_{1}

és

F_{2}

ordinátája 0-tól különböző és egyenlő előjelű, azaz

α_{1}

) vagy

x_{0} + y_{0} < 0

, azaz

y_{0} < - x_{0}

α_{2}

) vagy

x_{0} + y_{0} - x_{0}^{3} > 0

, azaz

y_{0} > x_{0}^{3} - x_{0}

akkor

φ (t)

görbéje csak egyszer metszi át a

t

tengelyt ‐ valamelyik emelkedő szakaszában ‐, ezért (1)-nek 1 valós gyöke van, és így

P_{0}

-on egyetlen érintője megy át az eredeti görbének. (Ti. az

α_{1}

esetben a minimum után, valamiyen

t > x_{0}

abszcisszán metszi át a

t

tengelyt

φ (t)

görbéje, az

α_{2}

esetben pedig a maximum előtt, valamilyen

t < 0

abszcisszán.)
Az

α_{1}

föltételt teljesítő

P_{0}

pontok az

y = - x

és

x > 0

föltételekkel jellemzett

i_{+}

félegyenes alatt vannak, az

α_{2}

föltételt teljesítők pedig az eredeti görbének

x > 0

íve,

g_{+}

fölött (1. ábra).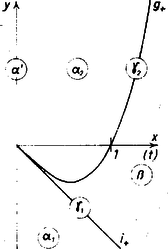

1. ábra

α'

) Lényegében ugyanide vezet

x_{0} = 0

esete is, amikor

φ' (t)

sehol sem negatív,

φ (t)

-nek nincs szélső értéke, görbéje állandóan emelkedik, és (1) így egyszerűsödik :

\begin{matrix} 2 t^{3} + y_{0} = 0, \end{matrix}

amit bármilyen

y_{0}

érték esetén csak egy

t

érték elégít ki.

β

) Ha

F_{1}

és

F_{2}

, a

t

tengely két oldalán adódik, vagyis a két ordináta 0-tól különböző és ellentétes előjelű :

\begin{matrix} x_{0} + y_{0} > 0 és x_{0} + y_{0} - x_{0}^{3} < 0 \end{matrix}

(természetesen ismét

x_{0} > 0)

, akkor

φ (t)

görbéjének

F_{1}

előtti,

F_{1}

és

F_{2}

közti, valamint

F_{2}

utáni íve külön‐külön átmetszi a

t

tengelyt, (1)-et 3 (különböző)

t

érték elégíti ki, tehát

P_{0}

-on az eredeti görbének 3 (különböző) érintője halad át. Az előbbiekhez hasonlóan ekkor

P_{0}

i_{+}

félegyenes fölött és a

g_{+}

görbeív alatt, vagyis köztük van.

γ

) Végül ha egyik fordulópont a

t

tengelyen adódik, akkor a másik alatta, ill. fölötte van, a tengelyen adódónak az ordinátája 0, azaz

vagy

γ_{1})

x_{0} + y_{0} = 0

, vagy

γ_{2})

x_{0} + y_{0} = x_{0}^{3}

Eszerint a görbe a fordulópontban ‐ mint az egyik emelkedő szakasz végpontjában ‐ érinti a

t

tengelyt, a másik emelkedő szakaszával pedig átmetszi, tehát (1)-et két különböző

t

érték elégíti ki, és

P_{0}

-on két érintője megy át az adott görbének. A

γ_{2}

esetben

y_{0} = x_{0}^{3} - x_{0}

, tehát

P_{0}

g_{+}

íven van,

γ_{1}

esetében pedig az

i_{+}

félegyenesen.
Vegyük észre, hogy a kiemelt szerepet játszó

i_{+}

félegyenes, és az origóra vonatkozó

i_{-}

tükörképe együtt az adott görbének az origóbeli érintőjét alkotják, hiszen

f' (0) = - 1

, másrészt hogy az origó görbénknek inflexiós pontja, mert

x < 0

és

x > 0

esetén egyaránt

f' (x) > - 1

. Ezek szerint az

i

egyenes a

g

görbének az inflexiós érintője. (Könnyű belátni, hogy több inflexiós érintője nincs görbénknek.)

Mindezek szerint a

g

görbe pontjain és

i

inflexiós érintőjének pontjain 2 érintője megy át a görbének ‐ kivéve a görbe inflexiós pontját, amelyen át csak egy, a kitüntetett érintő ; egyébként bármely az

y

tengellyel párhuzamos egyenes

g

és

i

közti szakaszának belső pontjain 3 érintő, egyéb pontjain 1 érintő megy át (2. ábra).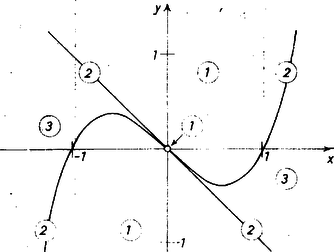

2. ábra

Ezzel a sík minden pontjára vonatkozóan megadtuk a választ.

Lakner Péter (Budapest, Berzsenyi D. Gimn., II. o. t.)

Megjegyzések. 1. A

γ)

eset két alesetében (1) így egyszerűsödik, ill. alakítható

γ_{1})

2 t^{3} - 3 x_{0} t^{2} = 2 t^{2} (t - \frac{3}{2} x_{0}) = 0

γ_{2})

2 t^{3} - 3 x_{0} t^{2} + x_{0}^{3} = 2 {(t - x_{0})}^{2} (t + \frac{x_{0}}{2})

Az előbbi szerint az (

x_{0}

- x_{0}

x_{0} \neq 0

ponton átmenő egyik érintő

i

, a másikra pedig az innen húzott érintő érintési pontjának abszcisszája

t = \frac{3}{2} x_{0}

Ez módot ad görbénk

(c, f (c))

c \neq 0

pontjában az érintő egyszerű megszerkesztésére : át kell mennie az inflexiós érintő

(\frac{2 c}{3}, - \frac{2 c}{3})

pontján.

Hasonlóan

γ_{2})

szerint az

(x_{0}, f (x_{0}))

ponton átmegy a

- \frac{x_{0}}{2}

abszcisszájú pontbeli érintő, tehát fordítva : a

(c, f (c))

pontbeli érintőt úgy is megkaphatjuk, hogy pontunkat összekötjük a

(- 2 c, f (- 2 c))

ponttal (3. ábra, 214. old.).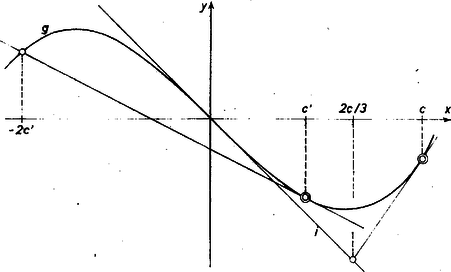

3. ábra

2. Meg lehet mutatni, hogy megállapításaink bármely

y = a x^{3} + b x^{2} + c x + d

egyenletű görbére (ún. harmadfokú parabolára) érvényesek, ha az origó helyén a mindenkori inflexiós pontot,

i

helyén az ottani érintőt értjük.
3. A megoldások nagy része (1) átalakításával eljutott a harmadfokú egyenlet szokásos

x^{3} + p x + q = 0

"redukált'' alakjára ; ennek

{(\frac{p}{3})}^{3} + {(\frac{q}{2})}^{2}

diszkriminánsát mint

x_{0}

és

y_{0}

kifejezését sikerült szorzattá alakítaniuk és a két tényező előjelkombinációinak vizsgálatával értek célhoz. (Nem lényegesen különböző az

x^{3} + 3 p x + 2 q = 0

és

p^{3} + q^{2}

diszkrimináns törtek látszólagos elkerülésével, hiszen nem szorítkozhatunk a

p

q

egész értékpárokra.) Ezzel lényegében az F. 1661. feladat megoldásában^{$^{*}$} bemutatott út fordítottját járták be.

^{$^{*}$}Milyen feltételt kell kielégíteniük a

p

q

együtthatóknak, hogy az

f (x) = x^{3} + p x + q

függvény szélső értékei ellentett előjelűek legyenek ? Lásd K. M. L. 39 (1989) 129.