Kezdőlap


Feladat:	F.1816	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1973/április, 160 - 161. oldal		PDF \| MathML
Témakör(ök):	Differenciálási szabályok, Elemi függvények differenciálhányadosai, Magasabbrendű deriváltak, Függvényvizsgálat differenciálszámítással, Feladat
Hivatkozás(ok):	Feladatok: 1972/március: F.1816

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Görbe inflexiós pontjának fogalmát az $x^{3}$ függvény görbéjéhez az $x = 0$ abszcisszájú pontban fektetett érintő példáján ismertük meg a tankönyvből. Itt az érintő maga az $x$ tengely, és ha $x$ növekedve halad át a $0$ értéken, akkor a görbe az érintő alsó partjáról áthajlik a felső partjára. Ezt így is mondhatjuk: tekintsük a görbe és az inflexiós pontbeli érintő ugyanazon abszcisszájú pontjaira nézve az ordinátákat, ezek különbsége $x < 0$ esetén negatív, $x > 0$ esetén pozitív. Ezt az előjelváltozást tekintjük egy tetszőleges $f (x)$ függvénygörbe inflexiós pontja és inflexiós érintője jellemző tulajdonságának; pontosabban így: $[u, f (u)]$ , akkor inflexiós pontja az $y = f (x)$ görbének, ha véve az $u$ -beli érintő

\begin{matrix} y = f (u) + f' (u) (x - u) \end{matrix}

egyenletét, az

\begin{matrix} f i x) - [f (u) + f' (u) (x - u)] = g (x) \end{matrix}

különbség előjele az

u

helyen áthaladva megváltozik [magán az

u

helyen értelemszerűen

g (u) = 0

a különbség értéke]. ‐ Természetesen csak differenciálható

f

-ekre gondolunk.
Az előjelváltozás azt jelenti, hogy

g (x)

görbéje az

u

helyen áthaladva áttér az

x

tengely alsó partjáról a felsőre vagy a felsőről az alsóra. Tehát ez a görbe

u

előtt is, utána is emelkedik, illetve előtte is, utána is süllyed. Eszerint ‐ mivel

f

-fel együtt

g

is differenciálható ‐

g' (x)

u

után ugyanolyan jelű, mint volt

u

előtt.
Mármost ha az

u

hely egy bizonyos környezetében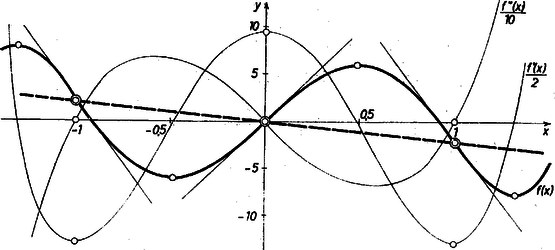

\begin{matrix} g' (x) = f' (x) - f' (u) > 0, x \neq u, \end{matrix}

ez azt jelenti, hogy akár

x < u

, akár

x > u

, a derivált értéke nagyobb, mint

f' (u)

, tehát a deriváltnak

x = u

-ban minimuma van. Hasonlóan, ha a környezetben

g' (x) < 0

és

x \neq u

, akkora deriváltnak

u

-ban maximuma van. Mindkét lehetőséghez egyaránt szükséges, hogy

\begin{matrix} [g' (x)]' = [f' (x)]' = f'' (x), \end{matrix}

azaz

f

második deriváltja az

u

helyen

0

legyen. Feladatunkban

\begin{matrix} f'' (x) = (45 x^{4} - 90 x^{2} + 19)' = 180 x^{3} - 180 x = 180 x (x - 1) (x + 1) = 0 \end{matrix}

x = - 1

x = 0

és

x = 1

helyeken teljesül, és most meg kell vizsgálnunk, van-e valóban e helyeken maximum vagy minimum. ‐ A derivált így alakítható:

\begin{matrix} 45 x^{4} - 90 x^{2} + 19 = 45 {(x^{2} - 1)}^{2} - 26. \end{matrix}

A változó tag az

x = \pm 1

helyek kivételével mindenütt pozitív, és e két helyen

0

, tehát e két helyen

f' (x)

-nek valóban szoros értelemben vett minimuma van. Ha pedig

| x | < 1

és

x \neq 0

, akkor

| x^{2} - 1 | < 1

, a változó tag kisebb, mint

45

, az

x = 0

helyen pedig egyenlő

45

-tel, tehát

f' (x)

-nek

x = 0

-ban valóban szoros értelemben vett maximuma van.

Ez a fentiek szerint elegendő

g (x)

előjelváltozásához, ahhoz, hogy az

f (x)

görbe

\begin{matrix} (- 1, 2), (0, 0), (1, - 2) \end{matrix}

pontjai inflexiós pontok legyenek. Számítás nélkül látható, hogy ez a három pont rajta van az

y = - 2 x

egyenesen. ‐ Ezzel a bizonyítást befejeztük.