Kezdőlap


Feladat:	F.1814	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1972/november, 141 - 143. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1972/február: F.1814

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A konvexség azt jelenti, hogy a $C A$ átló szétválasztja a $D$ , $B$ csúcsokat, a $B D$ átló pedig $C$ -t és $A$ -t, eszerint $D C B ∢ = D C A ∢ + A C B ∢ = 75^{\circ}$ , és hasonlóan $C D A ∢ = C D B ∢ + B D A ∢ = 75^{\circ}$ . Most a négyszögnek mind a négy részháromszögében csupán két‐két független adatot ismerünk.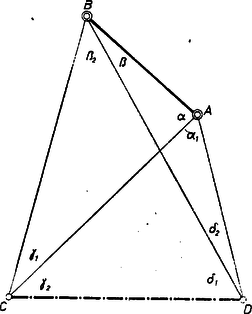

Megoldhatjuk azonban feladatunkat úgy, hogy kifejezzük a

C D A

és

C D B

háromszögből

C A

-t, ill.

C B

-t (a sinustétel alapján) a kérdezett

C D

oldallal és ismert szögek függvényeivel, majd e két kifejezés felhasználásával az

A B C

háromszögből az ismert

A B

-t fejezzük ki (a cosinustétel alapján) a kérdezett

C D

oldallal és ismert szögek szögfüggvényeivel. Ezáltal ugyanis egyenletet kapunk

C D

-re:

\begin{matrix} A B^{2} = C A^{2} + C B^{2} - 2 C A \cdot cos B C A ∢ = \\ = \frac{C D^{2} sin^{2} C D A ∢}{sin^{2} C A D ∢} + \frac{C D^{2} sin^{2} C D B ∢}{sin^{2} C B D ∢} - \frac{2 \cdot C D^{2} sin C D A ∢ sin C D B ∢ cos B C A ∢}{sin C A D ∢ sin C B D ∢}, \end{matrix}

amiből, áttérve a szögeknek az ábra szerinti egyszerűbb jelölésére

\begin{matrix} C D^{2} = \frac{A B^{2}}{N}, C D = \frac{A B}{\sqrt[]{N}}, ahol \\ N = \frac{sin^{2} (δ_{1} + δ_{2})}{sin^{2} (γ_{2} + δ_{1} + δ_{2})} + \frac{sin^{2} δ_{1}}{sin^{2} (γ_{1} + γ_{2} + δ_{1})} - \frac{2 sin δ_{1} sin (δ_{1} + δ_{2}) cos γ_{1}}{sin (γ_{2} + δ_{1} + δ_{2}) sin (γ_{1} + γ_{2} + δ_{1})} . \end{matrix}

Számadatainkkal

\begin{matrix} N = \frac{4 - \sqrt[]{3}}{6}, C D = 25 \sqrt[]{\frac{6 (4 + \sqrt[]{3})}{13}} = 40, 66 egység . \end{matrix}

Megjegyzések. 1. Természetesen a

D A

és

D B

távolságok kifejezéseivel is kifejezhettük volna

A B

-t, majd ezzel

C D

-t.
2. Feladatunkban a numerikus számítást elvégezhettük trigonometriai táblázat nélkül, mert mind a négy szögadat ún. ,,nevezetes szög'', és ilyenek a felhasznált összegeik is.
3. A feladat a gyakorlati trigonometriában (geodéziában) is szerepel, mint az

A

B

C

és

D

tereppontok közti 6 távolság kapcsolatának kérdése, ha ismerjük egyrészt az

A

és

B

alappontok távolságát, másrészt a meghatározandó

C

és

D

pontokban a másik három pont felé mutató irányok közti szögeket. A feladatot Hansen‐féle hátrametszésnek nevezik. A tankönyvből ismert hátrametszéshez¹ hasonlítva tekinthetjük egyedül

C

-t meghatározandó pontnak,

D

-t mintegy a hiányzó harmadik alappont pótlására önkényesen fölvett pontnak, amely azáltal válik használhatóvá, hogy benne elvégezhetjük ugyanazokat a szögméréseket, mint

C

-ben.
Gyakorlati feladatban a mért szögadatok tetszés szerintiek lehetnek, ilyenek mellett a fenti

N

számítása nehézkes a végzendő több különféle művelet miatt. Bemutatjuk alább a megoldás egy átalakítását abból a korból, amikor a számolások megkönnyítésének majdnem kizárólagos eszközei a logaritmus‐táblázatok voltak.
Egyébként feladatunk szerkesztéssel való megoldását a Gy. 1419. gyakorlat fogja adni.

II. megoldás. Először az ismert

A B

oldalra támaszkodó

B A C ∢ = α

és

A B D ∢ = β

szögeket számítjuk ki. Összegük nyilvánvalóan

α + β = γ_{2} + δ_{1}

, ismert. Az

\begin{matrix} \frac{A B}{A D} \cdot \frac{B C}{B A} \cdot \frac{C D}{C B} \cdot \frac{D A}{D C} = 1 \end{matrix}

azonosságból a sinustétel alapján

\begin{matrix} \frac{sin δ_{2}}{sin β} \cdot \frac{sin α}{sin γ_{1}} \cdot \frac{sin β_{2}}{sin δ_{1}} \cdot \frac{sin γ_{2}}{sin α_{1}} = 1, \end{matrix}

és az addíció tétel alkalmazásával

\begin{matrix} sin α = \frac{sin α_{1} sin γ_{1} sin δ_{1}}{sin β_{2} sin γ_{2} sin δ_{2}} sin β = K sin β = K sin (γ_{2} + δ_{1} - α) = \\ = K sin (γ_{2} + δ_{1}) cos α - K cos (γ_{2} + δ_{1}) sin α, \\ ctg α = \frac{1 + K cos (γ_{2} + δ_{1})}{K sin (γ_{2} + δ_{1})} = ctg (γ_{2} + δ_{1}) + \frac{sin (γ_{1} + γ_{2} + δ_{1}) sin γ_{2} sin δ_{2}}{sin (γ_{2} + δ_{1} + δ_{2}) sin γ_{1} sin δ_{1} sin (γ_{2} + δ_{1})}, \end{matrix}

és itt a második tag kiszámítása trigonometriai logaritmustáblázat használatával csak összeadást‐kivonást igényel. (Asztali ‐ kézi vagy elektromechanikus ‐ számológépen is könnyebb a számítása, mert csak szorzás, osztás fordul elő benne.)

α

és

β

ismeretében a négy pont közti 5 további szakasz a sinustétel alapján számítható, vagyis a cosinustételnél kényelmesebben.

Megjegyzés. Használtuk a ,,kényelmes'' számolás kifejezést, és némelyeknek talán furcsának tűnik ez az összekapcsolás. De talán megérzik, hogy csak azt szokás érteni ezen: a számítási elv (a végképlet) megállapítása után a numerikus végrehajtással kevesebb a probléma.

¹Czapáry E.‐Horvay K.‐Pálmay L.: Matemetika a gimn. III. o. számára, Tankönyvkiadó, Budapest, 1968., 68. oldal.