Feladat: F.1810 Korcsoport: 18- Nehézségi fok: átlagos
Füzet: 1973/szeptember, 2 - 4. oldal  PDF  |  MathML 
Témakör(ök): Nevezetes azonosságok, Másodfokú (és arra visszavezethető) egyenletek, Egészrész, törtrész függvények, Függvényvizsgálat, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):Feladatok: 1972/február: F.1810

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha k≦x<k+1 (k egész), akkor {x}=x-k, tehát

f(x)=x2-(x-k)2+x+|x2-1|,(1)
azaz
f(x)=|x2-1|+(2k+1)x-k2(2)
ezért függvényünk képe parabolaívekből tevődik össze, hiszen az |x2-1| kifejezés vagy x2-1, vagy -x2+1.
A (2)-ből azonnal leolvashatjuk, hogy az x=k helyen az f(x) helyettesítési értéke megegyezik jobb oldali határértékével és e közös érték: |k2-1|+k2+k, a bal oldali határérték pedig |k2-1|+k2+k-1. Így függvényünk az egész helyeken jobbról folytonos és bal oldali határértéke 1-gyel kisebb, mint a helyettesítési értéke, azaz 1 egységgel felugrik.
a) Ha k≧1, azaz x≧1, akkor (2)-ből teljes négyzetté való kiegészítéssel kapjuk, hogy
f(x)=(x+k+12)2-(2k2+k+54).(3)
Így k≧1 esetén f(x) szigorúan monoton növekvő a [k,k+1) intervallumokban, hiszen ezekben x+k+12>0. Figyelembe véve az ugrásokról mondottakat, megállapíthatjuk, hogy x≧1 esetén f(x) szigorúan monoton növekvő, tehát itt szélső értéke, s f(1)=2 miatt zérushelye nincsen.
b) Ha k=0, azaz 0≦x<1, akkor
f(x)=54-(x-12)2,
amiből leolvasható, hogy az x0=12 helyen maximum van, és zérushely nincsen (hiszen ekkor |x-12|≦12, s így f(x)≧1).
c) Ha k=-1, azaz -1≦x<0, akkor
f(x)=14-(x+12)2,
tehát az x1=-12 helyen maximum van és x1*=-1 zérushely (több zérushely itt nincsen, hiszen -1<x<0 esetén
|x+12|<12,s ekkorf(x)>0).

 

 

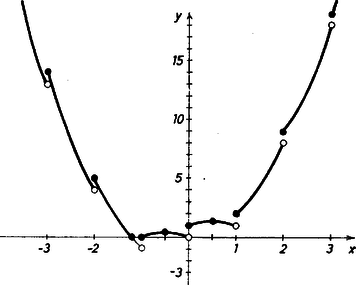d) Ha k<-1, azaz x<-1, akkor f(x)-re ismét a (3) előállítás érvényes, tehát f(x) szigorúan monoton csökkenő a [k,k+1) intervallumokban, hiszen esetünkben x+k+12<0. Így ebben az esetben szélsőérték csak az x-k=k(k=-2,-3,...) helyeken lehet. Ezek a helyek maximum helyek, hiszen ha k a (-1)-nél kisebb egész szám, akkor van olyan környezete, amelyben f(k) a legnagyobb függvényérték (mert az x=k helyen a bal oldali határérték f(k)-1, s ezért van olyan δ(0<δ<1), hogy f(x)<f(k), ha k-δ<x<k, másrészt láttuk, hogy f(x)<f(k), ha k<x<k+1, tehát mindig f(k)>f(x), ha x a k szám δ sugarú környezetébe esik és x≠k).
A fentiekből az is következik, hogy k<-1 esetén a [k,k+1) intervallumban csak akkor lehet zérushely, ha f(x)-nek a (k+1) helyen vett bal oldali határértéke negatív, azaz
|(k+1)2-1|+(k+1)2+(k+1)-1=k(2k+5)+1<0.
Így zérushely csak a [-2,-1] intervallumban lehet, amit (3)-ból könnyen meg is kaphatunk a k=-2 értékkel:
(x-32)2-294=0,
azaz
x2*=3-292=-1,193.

Összefoglalva: megállapítottuk, hogy az (1) függvény lokális maximum helyei: x0=12,x1=-12,xk=-k(k=2,3,...); lokális minimum helye nincsen, és két zérushelye van, ezek: x1*=-1 és x2*=-1,193.