Kezdőlap


Feladat:	F.1807	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1973/január, 17 - 18. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszög alapú gúlák, Kocka, Térfogat, Szélsőérték-feladatok differenciálszámítás nélkül, Térelemek és részeik, Feladat
Hivatkozás(ok):	Feladatok: 1972/január: F.1807

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egyszerűbben dolgozhatunk, ha a kérdést így mondjuk ki: ,, $λ$ mely értékénél a legnagyobb a kocka lemetszett részeinek együttes térfogata ?'' ‐ továbbá ha az élek két részét nem egymáshoz viszonyítjuk, hanem mindegyiket az eredeti kockaélhez. Így az $X Y$ él $λ$ arányú $Z$ osztópontjára

\begin{matrix} X Z = p = \frac{λ}{λ + 1} \cdot X Y, Z Y = q = \frac{1}{λ + 1} \cdot X Y és p + q = a, \end{matrix}

(1)

ahol

a

a kocka éleinek hosszát jelöli.
A lemetszett test mind a 8 kockacsúcs esetében háromoldalú gúla, és térfogata a kockával közös csúcsába befutó (

p

vagy

q

hosszúságú) élek szorzatának

1 / 6

része. Az első 8 felsorolt élben mind a 8 kockacsúcs egyszer

X

, egyszer

Y

szerepét kapta, eddig tehát mind a 8 csúcs egy

p

és egy

q

hosszúságú élrész közös pontja. Így pedig az utolsónak vett 4 él kezdőpontjaiban:

A

-ban,

B_{1}

-ben,

C

-ben és

D_{1}

-ben két

p

és egy

q

hosszúságú élrész fut össze, a többi 4 csúcsba pedig egy

p

és két

q

hosszúságú élrész. Ezek szerint a lemetszett gúlák együttes térfogata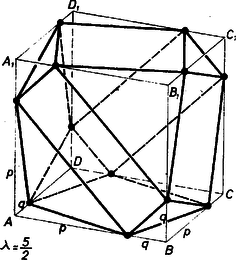

1. ábra

\begin{matrix} V = \frac{4}{6} p^{2} q + \frac{4}{6} p q^{2} = \frac{2 a}{3} p q, \end{matrix}

és nyilvánvalóan elég megkeresnünk azt a

λ

értéket, amely mellett az állandó

a

összegű

p

és

q

részek szorzata a legnagyobb. A

p q = p (a - p)

másodfokú függvény maximuma a

p = \frac{a}{2}

helyen van, ekkor

p = q

, és (1) alapján a keresett arányszám

λ = 1

, vagyis a kocka minden élén a felezőpontot vesszük osztáspontnak. ‐ Ezzel az előrebocsátottak szerint a feladatot megoldottuk. (A visszamaradt test térfogata a kockáénak

5 / 6

része.)

Megjegyzés. A

λ = 1

esetben a visszamaradó testet 6 négyzet és 8 szabályos háromszög határolja. Ha benne a háromszögek csúcsait tükrözzük a szemközti oldal felezőpontjára, egy szabályos oktaéder csúcsait kapjuk. (2. ábra).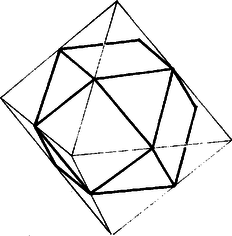

2. ábra