Kezdőlap


Feladat:	F.1794	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1974/november, 107 - 109. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Terület, felszín, Térelemek és részeik, Vektorok felbontása összetevőkre, Vektorok skaláris szorzata, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1971/november: F.1794

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tekintsük az $O$ csúcsú, $e$ tengelyű, $60^{\circ}$ -os fél nyílásszögű egyenes körkúpot. A feltétel szerint mindkét egyenes illeszkedik a kúp palástjára. Válasszuk meg a kúp alkotóját egységnyinek, valamint legyen az $S_{1}$ síkkal $45^{\circ}$ -os szöget bezáró egyenes $O B$ , a $30^{\circ}$ -os szöget bezáró egyenes $O C$ , ahol $O B$ , valamint $O C$ a kúp alkotói. Az egyenes körkúp alapjának középpontja legyen $M$ . Vetítsük a $B$ és $C$ pontokat merőlegesen az $S_{1}$ síkra, a vetületek legyenek $D$ , illetv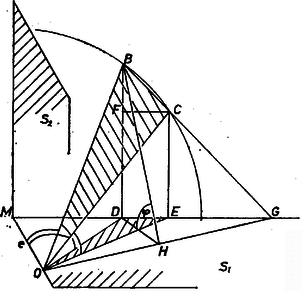e $E$ .

1. ábra

Feladatunk az

O B C

, valamint

O D E

háromszögek síkjai szögét meghatározni. De az

O D E

háromszög merőleges vetülete az

O B C

háromszögnek, így területe éppen az

O B C

háromszög területe szorozva a két sík hajlásszögének koszinuszával, azaz

φ

-vel jelölve a keresett szöget:

\begin{matrix} cos φ = \frac{T_{O D E}}{T_{O B C}} . \end{matrix}

(1)

Mivel az alkotó egységnyi hosszú, az

O B M

O B D

és

O C D

derékszögű háromszögekben a befogók hosszát könnyen meghatározhatjuk:

\begin{matrix} O M = cos 60^{\circ} = \frac{1}{2}, B D = sin 45^{\circ} = \frac{\sqrt[]{2}}{2}, C E = sin 30^{\circ} = \frac{1}{2} \end{matrix}

valamint

\begin{matrix} O D = cos 45^{\circ} = \frac{\sqrt[]{2}}{2}, O E = cos 30^{\circ} = \frac{\sqrt[]{3}}{2} . \end{matrix}

O B C

és

O D E

háromszögek két-két oldalát ismerjük, a harmadik oldalt a fenti adatokból már számíthatjuk. Először

D E

-t határozzuk meg:

\begin{matrix} M E = \sqrt[]{O E^{2} - M O^{2}} = \frac{\sqrt[]{2}}{2}, M D = \sqrt[]{O D^{2} - O M^{2}} = \frac{1}{2}, \\ D E = M E - M D = \frac{\sqrt[]{2} - 1}{2} . \end{matrix}

Így

\begin{matrix} T_{O D E} = \frac{1}{2} \cdot D E \cdot O M = \frac{1}{8} (\sqrt[]{2} - 1) . \end{matrix}

B C

meghatározásához vetítsük merőlegesen

C

-t

B D

-re. A vetületet jelölje

F

\begin{matrix} C F = E D = \frac{\sqrt[]{2} - 1}{2}, B F = B D - F D = B D - C E = \frac{\sqrt[]{2} - 1}{2} = C F . \end{matrix}

Azt kaptuk, hogy

B F C

egyenlő szárú derékszögű háromszög, tehát

\begin{matrix} B C = \sqrt[]{2} C F = \frac{2 - \sqrt[]{2}}{2} . \end{matrix}

O B C

egyenlő szárú háromszög magassága

\sqrt[]{O B^{2} - {(\frac{B C}{2})}^{2}} = \frac{\sqrt[]{10 + 4 \sqrt[]{2}}}{4}

, és így

\begin{matrix} T_{O B C} = \frac{1}{2} \cdot \frac{2 - \sqrt[]{2}}{2} \frac{\sqrt[]{10 + 4 \sqrt[]{2}}}{4} = \frac{1}{8} (\sqrt[]{2} - 1) \cdot \sqrt[]{5 + 2 \sqrt[]{2}} . \end{matrix}

Végül (1)-ből:

\begin{matrix} cos φ = \frac{\frac{1}{8} (\sqrt[]{2} - 1)}{\frac{1}{8} (\sqrt[]{2} - 1) \sqrt[]{5 + 2 \sqrt[]{2}}} = \frac{1}{\sqrt[]{5 + 2 \sqrt[]{2}}} = 0, 357, \end{matrix}

ahonnan

φ

-re

69^{\circ} 4'

-et kapunk.

Megjegyzés. Jelöljük a

B C

D E

egyenesek metszéspontját

G

-vel. A

B D G

háromszög hasonló a

B F C

háromszöghöz, és ez az utóbbi egyenlő szárú, emiatt

D G = D B = \frac{\sqrt[]{2}}{2}

. Tehát az

O D G

háromszög is egyenlő szárú, jelöljük az alapjának a felezőpontját

H

-val. Könnyen látható, hogy a

B D H

háromszög

H

-nál levő szöge egyenlő a keresett

φ

szöggel. Mivel

O G^{2} = \frac{1}{4} + \frac{{(\sqrt[]{2} + 1)}^{2}}{4} = \frac{2 + \sqrt[]{2}}{2}

\begin{matrix} D H^{2} = O D^{2} - O H^{2} = \frac{1}{2} - \frac{2 + \sqrt[]{2}}{8} = \frac{2 - \sqrt[]{2}}{8}, \end{matrix}

és így

\begin{matrix} tg φ = \frac{2}{2 - \sqrt[]{2}} \sqrt[]{4 + 2 \sqrt[]{2}} = 2, 613, φ = 69^{\circ} 4' . \end{matrix}

II. megoldás. Vegyünk fel egy koordináta-rendszert úgy, hogy az

O

pont legyen a koordináta-rendszer origója, az

e

félegyenes az

X

tengely pozitív ága, az

X

és

Y

tengelyek síkja pedig az

S_{1}

s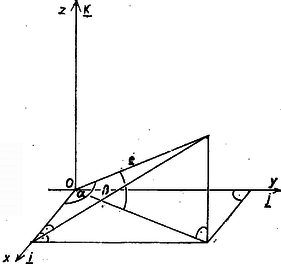ík.

2. ábra

Ha az

e

egységvektor az

X

tengellyel

α

szöget, az

X Y

tengelysíkkal

β

szöget zár be, akkor az

e

vektor tengelyirányú összetevői az ábra szerint

\begin{matrix} (cos α, ε \sqrt[]{1 - cos^{2} α - sin^{2} β}, sin β) . \end{matrix}

(2)

Itt

ε

-t

+ 1

-nek vagy

- 1

-nek kell megválasztanunk aszerint, hogy az

e

vektor az

S_{2}

sík melyik partjára esik. Ezek szerint, ha a feladatbeli két félegyenes irányvektora

a

, illetve

b

, akkor (2) szerint

\begin{matrix} a & = i cos 60^{\circ} + j ε \sqrt[]{1 - cos^{2} 60^{\circ} - sin^{2} 45^{\circ}} + k \cdot sin 45^{\circ} = \frac{1}{2} i + \frac{ε}{2} j + \frac{\sqrt[]{2}}{2} k . \\ b & = i cos 60^{\circ} + j ε \cdot \sqrt[]{1 - cos^{2} 60^{\circ} - sin^{2} 30^{\circ}} + k sin 30^{\circ} = \frac{1}{2} i + ε \frac{\sqrt[]{2}}{2} j + \frac{1}{2} k . \end{matrix}

Itt mindkét helyen

ε

-t ugyanannak kell megválasztanunk, mivel a két félegyenes ugyanabba a térnegyedbe esik. Az

a

és

b

vektorok által kifeszített sík normálvektora

\begin{matrix} n=a\timesb = - \frac{ε}{4} i + \frac{\sqrt[]{2} - 1}{4} j + ε \frac{\sqrt[]{2} - 1}{4} k . \end{matrix}

S_{1}

sík normálvektora éppen

k

. A kérdezett sík és

S_{1}

hajlásszöge megegyezik normálvektoraik hajlásszögével. A hajlásszög koszinuszát a skaláris szorzat definíciója alapján kaphatjuk meg:

\begin{matrix} | u \cdot v | = | u | \cdot | v | \cdot cos (u, v) - ből cos (u, v) = \frac{| u \cdot v |}{| u | \cdot | v |} \end{matrix}

azaz

\begin{matrix} cos φ & = \frac{| (- \frac{ε}{4} i + \frac{\sqrt[]{2} - 1}{4} j + ε \frac{\sqrt[]{2} - 1}{4} k) \cdot k |}{| - \frac{ε}{4} i + \frac{\sqrt[]{2} - 1}{4} j + ε \frac{\sqrt[]{2} - 1}{4} k | \cdot 1} = \\ = \frac{| ε | | \sqrt[]{2} - 1 |}{\sqrt[]{1^{2} + {(\sqrt[]{2} - 1)}^{2} + {(\sqrt[]{2} - 1)}^{2}}} = \frac{\sqrt[]{2} - 1}{\sqrt[]{7 - 4 \sqrt[]{2}}} = 0, 357, \end{matrix}

amiből

φ = 69^{\circ} 4'