Feladat: F.1783 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Asszonyi Sylvia 
Füzet: 1973/március, 97 - 100. oldal  PDF  |  MathML 
Témakör(ök): Egyéb sokszögek hasonlósága, Inverzió, Körök, Trapézok, Húrnégyszögek, Négyszögek szerkesztése, Feladat
Hivatkozás(ok):Feladatok: 1971/szeptember: F.1783

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a c és AB egyenesek metszéspontját M-mel, kisebbik szögüket θ-val (θ≦90∘). Mivel a keresett húrnégyszögben A és B, másrészt C és D egyező szerepet játszanak, a betűzést úgy választjuk, hogy MA<MB, a négyszög konvex, és így MD<MC, hiszen M kívül van a k körülírt körön.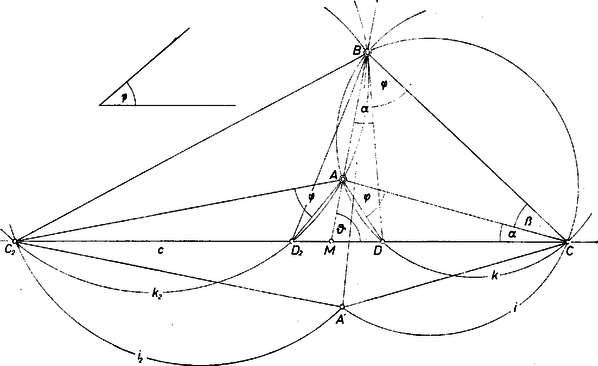

 

 

1. ábra
 

1. Először c -nek az MA félegyenessel θ szöget bezáró félegyenesén keressük D-t és C-t (1. ábra jobb oldali fele). Összefüggéseket keresünk a DA, AB szakaszok C-ből vett látószögei φ és θ között. Legyen DCA∢=α, ACB∢=β, ekkor a k-ra tekintettel DBA∢=α, az MBC háromszög szögeinek összege
θ+(α+β)+(φ+α)=180∘,
és innen
2α+β=180∘-θ-φ.(1)
Itt a jobb oldal ismert, a bal oldalnak pedig látószög jelentést tulajdoníthatunk. Legyen A tükörképe c-re A', ekkor A'CM∢=α, és 2α+β=A'CB∢, az A'B ismert szakasznak C-ből vett látószöge. Ebből C megszerkeszthető (az i látókörívet A'B-nek természetesen az M-et nem tartalmazó partján kell szerkesztenünk), ezután k az ABC háromszög körülírt köre, végül ennek c-vel való második metszéspontja D.
A kapott ABCD négyszög húrnégyszög, és benne
DAC∢=DBC∢=180∘-BMC∢-BCM∢-MBD∢=(180∘-θ)--(BCM∢+MCA'∢)-(180∘-θ)-(180∘-θ-φ)=φ,


hiszen MBD∢=ABD∢=ACD∢=A'CD∢=A'CM∢.
A C pont létrejön, hacsak (1) jobb oldalán (180∘-θ-φ)>0∘, azaz φ<180∘-θ, mert a kimetsző A'B körív két végpontja a c-nek két partján van. E föltétel teljesülése esetén mindig 1 megoldása van a feladatnak.
2. A fenti gondolat megismételhető c-nek másik félegyenesén. A változás csak annyi, hogy θ helyére (180∘-θ) lép, A'B-nek az (új) C2 pontból vett látszöge (θ-φ), és a látókörív az A'B egyenesnek M-et tartalmazó partján szerkesztendő. A fenti föltétel helyére φ<θ lép, emellett 1 megoldás van, különben nincs megoldás (1. ábra bal oldali fele), a megfelelő négyszög ABC2D2.
3. Ha éppen θ=90∘, akkor az utóbbi megoldás nyilvánvalóan az előbbinek tükörképe az AB egyenesre ‐ természetesen amennyiben φ hegyesszög.
4. Összefoglalva az eddigieket: ha M létezik és φ<θ≦90∘, akkor 2 megoldás van, ha θ<90∘ és θ≦φ<180∘-θ, akkor 1 megoldás van, végül φ≧180∘-θ esetén nincs megoldás.
5. Szerkesztésünk a c∥AB esetben is érvényes, azaz ha M nem létezik és 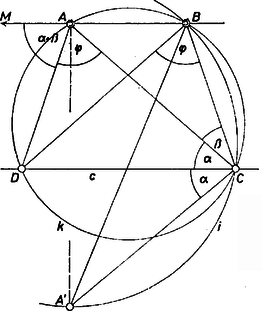θ=0∘.
 

2. ábra
 

Ugyanis ezt tudva is megkapjuk a módosult (1)-et, abból, hogy ACD∢=CAB∢, és a húrnégyszög miatt (α+β)+(φ+α)=180∘, tehát 2α+β=180∘-φ. Ekkor ABCD húrtrapéz, azaz tengelyszimmetrikus trapéz, és csak 1 megoldás van (2. ábra).
 

 Asszonyi Syilvia (Miskolc, Bláthy O. Villamosip. Techn., III. o. t.)
 

Megjegyzés. Egyszerűbb a szerkesztés a φ=90∘ speciális esetben. Ekkor CD-t A-ból derékszögben kell látnunk, eleve tudjuk tehát, hogy k középpontja a c-n van, mégpedig az AB szakasz felező merőlegese metszi ki belőle.
Erre az eredményre természetesen a fenti eljárásnak is el kell vezetnie, de várhatóan kissé hosszabb úton. Nézzük meg ezt a θ>0∘ esetben. Ekkor, az i látókörív középpontját Oi -vel jelölve,
A'OiB∢=2⋅A'CB∢=2(90∘-θ)=180∘-2θ=180∘-A'MB∢,
tehát Oi rajta van az A'BM háromszög köré írt körön. Másrészt eleve rajta van A'B felező merőlegesén, tehát Oi felezi e kör A'B ívét, ezért MOi felezi az A'MB szöget, tehát azonos magával c -vel. Oi tehát a c-n adódik, ezért az i-t tartalmazó A'BC kör átmegy A'-nek c -re való tükörképén, ami maga A, tehát e kör azonos a keresett k-val.
Ugyanezek a φ=90∘ és c∥AB (θ=0∘) esetben nyilvánvalóak.
 

II. megoldás. A keresett ABCD=N négyszög köré írt k kör O középpontjáról a következőket tudjuk. Egyrészt rajta van az AB szakasz f felező merőlegesén, másrészt ha φ<90∘, úgy DOC∢=2⋅DAC∢=2φ, ODC∢=90∘-φ, és O a c-nek A-t tartalmazó partján van; ha pedig 90∘<φ<180∘, akkor DOC∢=360∘-2φ, ODC∢=φ-90∘, és O a c másik partján van. (φ=90∘ esetén O a c, f egyenespár metszéspontja, lásd az előző megjegyzést is.) Ennyi elég ahhoz, hogy φ≠90∘ esetén N-hez középpontosan hasonló és egyező állású (pozitív nyújtási arányú) A*B*C*D*=N* négyszöget szerkeszthessünk, hacsak e transzformáció K középpontjaként f és c metszéspontját vesszük, föltéve, hogy ez létezik (azaz θ<90∘, ezt egyelőre föltesszük).
1. Így ugyanis D a KM félegyenesen lesz, ahol M az AB egyenes metszéspontja c -vel, D* is ezen adódik, az N* köré írt k* kör O* középpontja pedig f-en, és az O-ra fent mondottak O*-ra is érvényesek.
Ezek alapján a szerkesztés a következő (a 3a ábrán φ<90∘, a 3b ábrán φ>90∘, mindkettőn 0∘<θ<90∘, a 3b ábrán D* az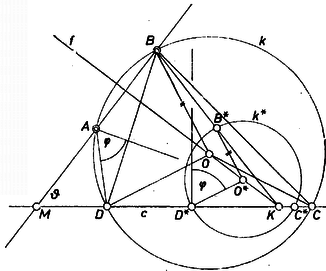onos M-mel).
 

3a. ábra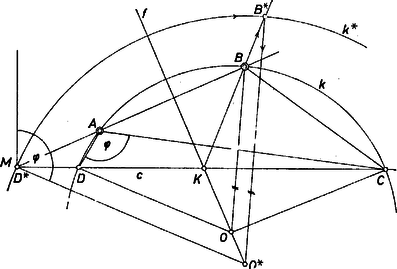
 

 

3b. ábra
 

A KM félegyenes tetszőleges D* pontjában merőleges félegyenest állítunk c -nek B-t tartalmazó partján. Ebből a D*K félegyenes felé fordulva fölmérjük φ-t, ennek új szára f-ből kimetszi O*-ot, k* sugara O*D*, és B*-ot k*-ból kimetszi a KB félegyenes. (Elég a továbbiak céljára A* és B* egyikét előállítani, egyébként A*-ot ugyanígy a KA félegyenes metszi ki.) Végül O-t a B-n átmenő, B*O*-gal párhuzamos egyenes metszi ki, és ekkor az O körüli, B-n átmenő körnek c -vel való metszéspontjai D és C.
O* a φ<90∘ esetben mindenesetre létrejön; φ>90∘ esetén pedig akkor, ha a felmért φ szög új szára metszi f-et: φ-90∘<90∘-θ, azaz 180∘-θ-φ>0∘, ahogyan az I. megoldásban láttuk.
Ha φ<90∘, és k* nem zárja magába K-t (C is a KM félegyenesen adódik), azaz 90∘-θ<90∘-φ, tehát φ<θ, akkor B* szerepére 2 pontot és N-re 2 megoldást kapunk ‐ ilyen helyzetre vezetne az 1. ábra adatrendszere (A, B, c kölcsönös helyzete és φ értéke). Ha k* átmegy K-n (φ=θ) vagy magába zárja (θ<φ<180∘-θ), akkor 1-et.
2. K akkor és csak akkor nem jön létre, ha AB⊥c. Ekkor f∥c, és elég, ha meggondolásunk elejét így módosítjuk: "toljuk el N-et c -vel párhuzamosan valamely N* helyzetbe'' (4. ábra).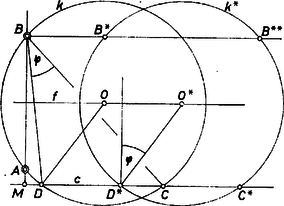
 

4. ábra
 

A c -n tetszőlegesen fölvett D*-ből kiindulva O*-ot, k*-ot (φ<90∘ esetén) a föntiekhez hasonlóan kapjuk, B*-ot (B**-ot) a B-n átmenő c -vel párhuzamos egyenes metszi ki k*-ból, végül a B*C*D* háromszöget a B*B→ vektorral a helyére toljuk. B* létrejön, mert B annyira van f-től, mint A, tehát közelebb van f-hez, mint a c -n levő D*, tehát távolsága kisebb, mint k* sugara. ‐ B**-ból persze az első megoldás tükörképét kapjuk.
 

Megjegyzés. Megoldható a feladat inverzió alkalmazásával is.