Kezdőlap


Feladat:	F.1782	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1972/október, 52 - 56. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Geometriai egyenlőtlenségek, Trigonometria, Körülírt kör, Terület, felszín, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1971/szeptember: F.1782

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Felhasználjuk, hogy a háromszög területe kifejezhető az oldalakkal és a körülírt kör $r$ sugarával:

\begin{matrix} t = \frac{a m_{a}}{2} = \frac{a b sin γ}{2} = \frac{a b}{4} \cdot \frac{2 r sin γ}{r} = \frac{a b c}{4 r} . \end{matrix}

(2)

(Az oldalak a háromszöggel együtt természetesen

r

-et is meghatározzák.) Felhasználjuk továbbá, hogy az

x^{3}

függvény szigorúan monoton növekvő, mert nincs olyan intervallum, melyben a deriváltja negatív vagy 0 volna. Ezek alapján az (1) állítást így alakítjuk:

\begin{matrix} 64 t^{3} = 4 t {(\frac{a b c}{r})}^{2} \leq 3 \sqrt[]{3} a^{2} b^{2} c^{2}, t \leq \frac{3 \sqrt[]{3}}{4} r^{2} = \frac{1}{2} \cdot (\sqrt[]{3} r) \cdot \frac{3 r}{2} . \end{matrix}

Az utolsó alakban felismerjük, hogy a (

\sqrt[]{3} r

) tényező a háromszögünk köré írt

k

körbe írható szabályos háromszög oldala,

3 r / 2

pedig annak magassága, tehát a jobb oldal a mondott szabályos háromszög

T

területét jelenti. Ennélfogva azt kell bizonyítanunk, hogy

\begin{matrix} t \leq T . \end{matrix}

(3)

Válasszuk úgy

A B C

háromszögünk szokásos betűzését, hogy legyen

a \leq b \leq c

. Ha itt mindkét összehasonlításban egyenlőség áll, akkor

A B C

szabályos háromszög, és (3)-ban egyenlőség áll. Az ellentétes esetben

a < c

, és a megfelelő szögekre

B A C ∢ < 60^{\circ} < A C B ∢

. Belátjuk, hogy ekkor (3) az egyenlőtlenség jelével érvényes.
Jelöljük a

B

csúcsnak az

A C

oldal felező merőlegesére vonatkozó tükörképét

B^{*}

-gal és

k

középpontját

O

-val (1. ábr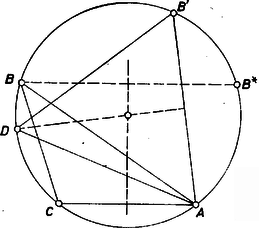a).

1. ábra

Ekkor

\begin{matrix} A O B^{*} ∢ & = C O B ∢ = 2 C A B ∢ < 120^{\circ}, és \\ A O B ∢ & = 2 A C B ∢ > 120^{\circ} \end{matrix}

(az utóbbi esetben

A O B ∢ k

-nak a

C

-t nem tartalmazó

A B

ívéhez tartozó középponti szögét jelöli). Ha tehát az

O A

sugarat az

A B C

háromszög körüljárásával megegyező irányban

O

körül

120^{\circ}

-kal elforgatjuk, közben átlépjük az

O B^{*}

sugarat, de nem érjük el az

O B

sugarat. Jelöljük a

120^{\circ}

-os forgatás után a sugár új végpontját

B'

-vel, ekkor előbbi megállapításunk szerint

B'

C

-t nem tartalmazó

B^{*} B

íven van, tehát távolabb van az

A C

egyenestől, mint

B

. Eszerint az

A B' C

háromszög

t_{1}

területe nagyobb

t

-nél.
A

k

kör

A B'

-től legtávolabbi pontja az

A B'

-re merőleges átmérőnek

A B'

-től távolabbi

D

végpontja, tehát

t_{1}

nem lehet nagyobb az

A B' D

háromszög területénél. Mivel pedig az

A B'

ívhez tartozó középponti szög

120^{\circ}

-os, azért az

A B' D

háromszög szabályos, és a területe

T

. Ezzel beláttuk, hogy

T \geq t_{1} > t

, ezt akartuk bizonyítani.

Megjegyzés. A fenti bizonyítás nem különbözik lényegesen attól, ami a (3) híres-nevezetes állításra pl. a következő helyen olvasható: H. Rademacher-O. Toeplitz: Számokról és alakzatokról. 2. kiadás. Középiskolai Szakköri Füzetek. Tankönyvkiadó, Budapest, 1954. 14‐16. oldal.

II. megoldás. Az állítást ismét átalakítjuk. (2) alapján a fentiekhez hasonlóan

\begin{matrix} \frac{a b c}{r} \leq \sqrt[]{3} \sqrt[3]{a^{2} b^{2} c^{2}}, azaz \sqrt[3]{a b c} \leq \sqrt[]{3} r . \end{matrix}

Ehhez elég belátni, hogy (poz. számok számtani és mértani közepe):

\begin{matrix} \frac{a + b + c}{3} \leq \sqrt[]{3} r, \end{matrix}

(4)

vagyis azt, hogy az

r

sugarú körbe írt háromszög kerülete legföljebb

3 \sqrt[]{3} r

, ami a fentiek szerint a beírt szabályos háromszög kerülete.
Ezt ugyanúgy láthatjuk be, mint az I. megoldásban (3)-at. Az ott használt jelölések mellett elég azt belátnunk, hogy

\begin{matrix} A B' + B' C > A B + B C, \end{matrix}

azaz hogy

\begin{matrix} 2 r sin 60^{\circ} + 2 r sin (α + γ - 60^{\circ}) > 2 r sin α + 2 r sin γ . \end{matrix}

Ez a

sin u + sin v = 2 sin \frac{u + v}{2} cos \frac{u - v}{2}

azonosság szerint ekvivalens a következőkkel:

\begin{matrix} sin \frac{α + γ}{2} cos \frac{α + γ - 120^{\circ}}{2} > sin \frac{α + γ}{2} cos \frac{γ - α}{2}, \\ \frac{α + γ}{2} - 60^{\circ} < \frac{γ - α}{2} . \end{matrix}

Ez pedig valóban igaz, mert jobb oldala így alakítható:

\begin{matrix} \frac{γ - α}{2} = \frac{α + γ}{2} - α, \end{matrix}

és

α < 60^{\circ}

. Hasonlóan láthatjuk be, hogy az

A B' D

háromszög kerülete legalább akkora, mint az

A B' C

kerülete.

Megjegyzések. 1. A (4) állítás ekvivalens a háromszögünk szögeire vonatkozó

\begin{matrix} \frac{sin α + sin β + sin γ}{3} \leq \frac{\sqrt[]{3}}{2} \end{matrix}

egyenlőtlenséggel. Erre adunk szemléletes értelmezést:

sin α, sin β

és

sin γ

sin x

függvényt ábrázoló görbe

α

β

, ill.

γ

abszcisszájú

A^{*}

B^{*}

C^{*}

pontjának ordinátája. Az abszcisszák pozitívok és összegük

π

. Így (4) bal oldala az

A^{*} B^{*} C^{*}

háromszög

S

súlypontjának ordinátája,

S

abszcisszája hasonlóan

σ = π / 3

, és a görbe

σ

abszcisszájú

S^{*}

pontjának ordinátája

\sqrt[]{3} / 2

, a (4) jobb oldalán álló szám. Eszerint (4) más szóval azt állítja, hogy

S

alatta van a

sin x

függvényt ábrázoló görbének, vagy éppen rajta van. (Ha

α, β, γ

közül kettő vagy mind a három egyenlő, akkor a mondott háromszög elfajul, ekkor szemléletesebb az

A^{*}

B^{*}

C^{*}

tömegpontrendszer súlypontjára gondolni, mindhárom pontba egyenlő tömeget téve;

A^{*} \equiv B^{*}

esetén

S

A^{*} C^{*}

szakaszon van.)
Ha

α < β < γ

, akkor

S

benne van az

A^{*} B^{*} C^{*}

háromszögben, ezért elég azt belátni, hogy a görbe (

0, π

) intervallumbeli ívének két pontját összekötő húr a görbe alatt halad (2. ábra, jobb áttekintés érdekében torzítással), a szokásos kifejezéssel: a

sin x

görbe ‐ és a függvény is ‐ ebben az intervallumban konkáv (ti. alulról, a pozitív

y

tengely irányába nézve).^{$^{*}$}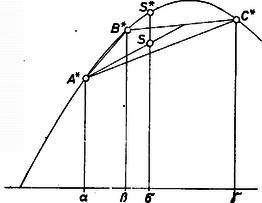

2. ábra

Ezt bizonyítjuk a

0 < α < β < γ

nagyságviszony esetében az

A^{*} C^{*}

húrra.
Állításunk azt jelenti, hogy a közbülső

B^{*}

pontra az

A^{*} B^{*}

egyenes emelkedése nagyobb, mint a

B^{*} C^{*}

egyenesé:

\begin{matrix} \frac{sin α - sin β}{α - β} > \frac{sin γ - sin β}{γ - β} . \end{matrix}

(5)

Ennek bizonyítására megmutatjuk, hogy

\begin{matrix} \frac{sin x - sin β}{x - β} {\begin{matrix} < cos β, ha π > x > β (I.) & (6) \\ > cos β, ha 0 < x < β (II.) \end{matrix} \end{matrix}

ebből

α < β < γ

figyelembevételével már adódik, hogy

cos β

értéke (5) bal oldalánál kisebb, jobb oldalánál nagyobb, tehát (5) igaz.
Deriváljuk a következő függvényt:

\begin{matrix} f (x) & = sin x - sin β - (x - β) cos β . \\ f' (x) & = cos x - cos β . \end{matrix}

Eszerint az (I.) intervallumban minden pontjában

f' (x) < 0

, a (II.) pontjaiban

f' (x) > 0

, és mivel

f (β) = 0

, azért (I.) és (II.) mindegyikében

f (x) < 0

. Ebből átrendezéssel és az osztásban

x - β

előjelét figyelembe véve adódik (6).
Mivel

cos β

sin x

görbe

B^{*}

-beli érintőjének iránytangense, azért az (5)-re adott bizonyításunk azt jelenti, hogy az érintő mind

x > β

, mind

x < β

esetén közte halad a

B^{*} C^{*}

és

A^{*} B^{*}

egyeneseknek.
2. Goniometriai bizonyítását adjuk a (6) pótlására alkalmas

\begin{matrix} cos α > \frac{sin β - sin α}{β - α} > cos β (0 < α < β < \frac{π}{2}) \end{matrix}

egyenlőtlenségnek. Mérjük föl az

O

középpontú, egységsugarú kör

O E

sugarától pozitív irányban az

E O P = α

és

E O Q = β

szögeket (3. ábra), húzzuk meg a kör

Q

-beli érintőjét az

O P

-vel való

T

metszéspontjáig, bocsássunk merőlegest

P

-ből és

Q

-ból

O E

-re ‐ talppontjuk

P_{1}

, ill.

Q_{1}

‐, továbbá

Q

-ból

O P

-re talppontja

S

‐, végül

S

-ből,

P

-ből és

T

-ből

Q Q_{1}

-re ‐ a talppontok rendre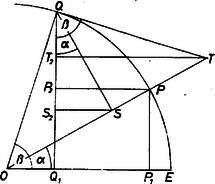

S_{2}, P_{2}, T_{2}

3. ábra

Így

Q_{1} Q S ∢ = α, Q_{1} Q T ∢ = β

, a pozitív hegyesszögekre ismert

sin x < x < tg x

egyenlőtlenséget a

Q O P = β - α

szögre alkalmazva

\begin{matrix} Q S < \hat{Q P} < Q T, \end{matrix}

továbbá

O S < O P < O T

, ennélfogva

Q_{1} S_{2} < Q_{1} P_{2} < Q_{1} T_{2}

, tehát

\begin{matrix} Q T_{2} < Q P_{2} < Q S_{2} . \end{matrix}

Ezek fölhasználásával

\begin{matrix} cos β \sim \sim \sim = \frac{Q T_{2}}{Q T} < \frac{Q P_{2}}{Q T} < \frac{Q P_{2}}{\hat{Q P}} = & \frac{Q Q_{1} - P P_{1}}{β - α} = \frac{sin β - sin α}{β - α} \sim \sim \sim \sim \sim \sim \sim \sim \sim < \frac{Q S_{2}}{\hat{Q P}} = \frac{Q S_{2}}{Q S} < cos α \sim \sim \sim \end{matrix}

és a hullámosan aláhúzott tagok éppen a fenti állításunkat adják.
Könnyű belátni, hogy bizonyításunk mindaddig érvényes, amíg

α < β < α + 90^{\circ}

, eszerint fenti állításunkat (

α, β

helyére rendre

β

-t,

γ

-t írva) csak olyan háromszögekre bizonyítja, amelyekre

γ - β < 90^{\circ}

. Másrészt elég a konvexséget a (

0, π / 2

) intervallumra bizonyítani, hiszen

sin x

képe a (

π / 2, π

) intervallumban amannak a tükörképe az

x = π / 2

egyenesre.

^{$^{*}$} Vö. a függvény konkávságának pusztán számviszonyokkal kifejezett definíciójával a P. 110. problémában. K. M. L. 43 (1971) 30. oldal.