Kezdőlap


Feladat:	F.1764	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1971/szeptember, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Határozott integrál, Terület, felszín, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1971/március: F.1764

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A$ fókuszú, $B C$ vezéregyenesű $p$ parabola csúcsérintője az $A A_{0}$ szakasz felező merőlegese, ahol $A_{0}$ az $A$ fókusznak a $B C$ tengelyen levő merőleges vetülete. Ez a felező merőleges az $A B$ , $A C$ oldalakat a $C_{0}$ , $B_{0}$ felezőpontjaikban metszi, hiszen minden, a fókuszt a vezéregyenessel összekötő szakaszt felez. A $p$ parabola a $B_{0} C_{0}$ csúcsérintőnek az $A$ -t tartalmazó oldalán van, az $A B C = H$ háromszögben levő része tehát az $A B_{0} C_{0}$ háromszögben is benne van.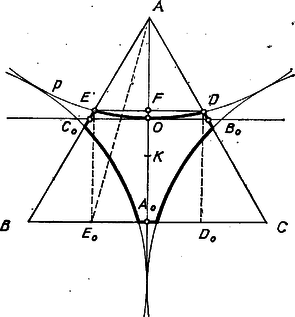

Hasonlóan kapjuk, hogy a

B

fókuszú,

C A

vezéregyenesű parabola

H

-beli része a

B C_{0} A_{0}

háromszögben, a

C

fókuszú,

A B

vezéregyenesű parabola

H

-beli része pedig a

C A_{0} B_{0}

háromszögben is benne van. Ezek szerint e három parabola belsejének nincs

H

-n belül közös része, az általuk le nem fedett rész területét megkapjuk, ha

H

területéből levonjuk az általuk külön-külön lefedett részek területét. Elegendő a

p

belseje által lefedett rész területét meghatározni, mert a másik két parabola által fedett részek területei egyenlők ezzel, hiszen e részek megkaphatók a

p

által fedett résznek a

H

háromszög

K

centruma körüli alkalmas irányú

120^{\circ}

-os forgatásával.
A

p

parabola az

A B

szakaszt abban az

E

pontjában metszi, melynek

B C

-től mért

E E_{0}

távolsága egyenlő

A E

-vel. Így az

A E E_{0}

háromszögben az

A E E_{0} ∢ = 90^{\circ} + 60^{\circ} = 150^{\circ}

E A E_{0} ∢ = 15^{\circ}

, vagyis

A E_{0}

felezi a

B A A_{0}

szöget. A szögfelezőre ismert tétel szerint

\begin{matrix} B E_{0} : E_{0} A_{0} = B A : A A_{0} = 1 : \frac{\sqrt[]{3}}{2}, \\ B E_{0} = 2 - \sqrt[]{3}, E E_{0} = 2 \sqrt[]{3} - 3. \end{matrix}

Az egyenlő oldalú háromszög és a parabola szimmetriája alapján ugyanekkora

C D_{0}

, ill.

D D_{0}

hossza, ahol

D_{0}

D

vetülete

B C

-n.
Jelöljük

p

csúcsát

O

-val,

E D

felezőpontját

F

-fel. Az

A D O E

idomot (amelynek a területét meg akarjuk határozni) az

E D

egyenes az

A D E

szabályos háromszögre és a

D E O D

lencse alakú idomra vágja szét. Az

A D E

háromszög területe:

\begin{matrix} t_{1} = \frac{\sqrt[]{3}}{4} D E^{2} = \frac{\sqrt[]{3}}{4} {(2 \sqrt[]{3} - 3)}^{2} = \frac{21 \sqrt[]{3}}{4} - 9. \end{matrix}

D E O D

lencse alakú idom területe (amint azt alább belátjuk) a

D E

alap és az

F O

magasság szorzatának

2 / 3

része:

\begin{matrix} t_{2} = \frac{2}{3} D E \cdot F O = \frac{2}{3} D E (E E_{0} - O A_{0}) = \frac{2}{3} (2 \sqrt[]{3} - 3) (2 \sqrt[]{3} - 3 - \frac{\sqrt[]{3}}{4}) = 13 - \frac{15 \sqrt[]{3}}{2} . \end{matrix}

Tehát az

A D O E A

idom területe:

\begin{matrix} t = t_{1} + t_{2} = 4 - \frac{9 \sqrt[]{3}}{4}, \end{matrix}

és

H

-ban a három parabola által le nem fedett terület:

\begin{matrix} T = \frac{\sqrt[]{3}}{4} - 3 t = 7 \sqrt[]{3} - 12 \sim 0, 1244. \end{matrix}

Be kell még bizonyítanunk, hogy

t_{2} = \frac{2}{3} D E \cdot F O

. Válasszuk a koordinátarendszer

x

tengelyének a

B_{0} C_{0}

egyenest,

y

tengelynek az

A A_{0}

egyenest. Ekkor

p

egyenlete

y = λ x^{2}

, ahol

λ

alkalmas konstans. Legyen az

E D

szakasz hossza

2 μ

, akkor

F O = λ μ^{2}

, és a parabola

D O E

íve alatti terület:

\begin{matrix} t_{3} = \int_{- μ}^{μ} λ x^{2} d x = {[\frac{λ x^{3}}{3}]}_{- μ}^{μ} = \frac{2}{3} λ μ^{3} . \end{matrix}

E D

szakasz alatti terület

\begin{matrix} t_{4} = F O \cdot E D = 2 λ μ^{3} \end{matrix}

t_{3}

ennek

1 / 3

része, tehát

t_{2}

2 / 3

része, amint azt bizonyítani akartuk.