Kezdőlap


Feladat:	F.1752	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1972/március, 103 - 106. oldal		PDF \| MathML
Témakör(ök):	Differenciálszámítás, Egyenesek egyenlete, Hiperbola egyenlete, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1971/január: F.1752

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az adott parabola egyenlete

\begin{matrix} y = {a x}^{2} \end{matrix}

(1)

ahol

a

tetszőleges pozitív szám. A parabola (

x_{0}

y_{0}

) koordinátájú pontjához tartozó érintő

m

meredeksége egyenlő az

{a x}^{2}

függvény

x_{0}

-beli deriváltjával:

\begin{matrix} m = 2 a x_{0}, \end{matrix}

(2)

és az illető érintő egyenlete, mindjárt

y_{0} = {a x}_{0}^{2}

helyettesítéssel, rendezéssel

\begin{matrix} y - y_{0} = 2 a x_{0} (x - x_{0}), y + {a x}_{0}^{2} = 2 a x_{0} x . \end{matrix}

(3)

Ha a sík tetszőleges

P (u, v)

koordinátájú pontjából érintőt akarunk húzni a parabolához, akkor meg kell keresnünk a parabolának azt (vagy azokat) az érintőjét (érintőit), amelyek átmennek

P

-n. Eszerint olyan

x_{0}

-t keresünk, amelyre a (3) egyenletű egyenes átmegy az

(u, v)

ponton, azaz teljesül:

\begin{matrix} v + {a x}_{0}^{2} = 2 a x_{0} u . \end{matrix}

(4)

Ez adott

(u, v)

pont esetén másodfokú egyenlet az

x_{0}

ismeretlenre. Mivel (4)-ből átrendezéssel az

\begin{matrix} a {(x_{0} - u)}^{2} = {a u}^{2} - v \end{matrix}

(5)

egyenletet kapjuk, azért (4)-nek akkor és csakis akkor van két (különböző) valós megoldása, ha

\begin{matrix} {a u}^{2} > v . \end{matrix}

(6)

(Ez a feltétel szemléletesen azt jelenti, hogy a

P (u, v)

pont a parabola

(u, {a u}^{2})

pontja alatt van, egyszerűen:

P

az (1) egyenletű parabola alatt van.)
Ha tehát

P

koordinátáira teljesül (6), akkor

P

-ből a parabolához két érintő húzható. Jelöljük ezek meredekségét

m'

-vel és

m''

-vel, ezek az illető egyeneseknek az

x

tengellyel bezárt

α'

és

α''

szögeinek a tangensei. A két érintő közti szög (ez megállapodás szerint a két egyenes által meghatározott szögek közül a

90^{\circ}

-nál nem nagyobbat jelenti) akkor

45^{\circ}

, ha

| α' - α'' | = 45^{\circ}

vagy

| α' - α'' | = 135^{\circ}

azaz

| tg (α' - α'') | = | \frac{tg α' - tg α''}{1 + tg α' tg α''} | = | \frac{m' - m''}{1 + m' m''} | = | tg (\pm 45^{\circ}) | = 1

Ez akkor, és csakis akkor teljesül, ha

\begin{matrix} {(m' - m'')}^{2} = {(1 + m' m'')}^{2} . \end{matrix}

(7)

Láttuk, hogy az

(u, v)

pontból húzott érintők érintési pontjának az

x'_{0}

x''_{0}

abszcisszái a (4) egyenlet gyökei, így (2) és a gyökök és együtthatók közti összefüggés alapján

\begin{matrix} m' + m'' = 2 a (x'_{0} + x''_{0}) = 4 a u, m' m'' = 4 a^{2} x'_{0} x''_{0} = 4 a v . \end{matrix}

(8)

Célszerű tehát (7)-et úgy átalakítani, hogy benne az

m'

m''

meredekségek összege és szorzata szerepeljen:

\begin{matrix} {(m' + m'')}^{2} - 4 m' m'' = {(1 + m' m'')}^{2} . \end{matrix}

Eszerint a

P (u, v)

pont akkor és csakis akkor tartozik a vizsgált mértani helyhez, ha az

(u, v)

koordinátákra teljesül (6), és a (7)-ből (8) alapján kapható

\begin{matrix} {(4 a u)}^{2} - 16 a v = {(1 + 4 a v)}^{2} \end{matrix}

(9)

egyenlet. Ez utóbbiból már következik (6), hiszen (9) bal oldalán

16 a (a u^{2} - v)

áll, ahol a zárójelbeli kifejezés (6) két oldalának a különbsége, és (9) jobb oldalán pozitív szám áll. (Nem lehet ugyanis 0 sem a (9) jobb oldalának az értéke, mert

v = - 1 / 4 a

mellett (9) bal oldalának az értéke minden

u

-ra pozitív volna.) Mármost (9)-et rendezve ezt kapjuk:

\begin{matrix} {(v + \frac{3}{4 a})}^{2} - u^{2} = \frac{1}{2 a^{2}} . \end{matrix}

(10)

Ez tehát a vizsgált mértani hely egyenlete (1. ábra).^{$^{*}$}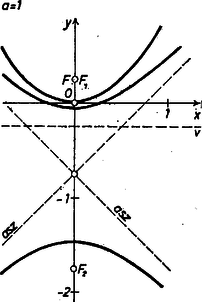

1. ábra

Megjegyzés. Láttuk, hogy a parabolához a

P (u, v)

külső pontból húzott érintők érintési pontjainak az abszcisszái a (4) egyenlet gyökei. (4)-et (5) alapján még az

\begin{matrix} {(x_{0} - u)}^{2} + {(- \frac{1}{4 a} - v)}^{2} = {(0 - u)}^{2} + {(\frac{1}{4 a} - v)}^{2} \end{matrix}

(11)

alakban is felírhatjuk, eszerint az

(x_{0}, - 1 / 4 a)

pont rajta van az

(u, v)

középpontú és a

(0, 1 / 4 a)

ponton átmenő

k

körön (2. ábra).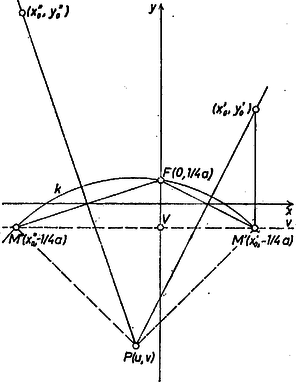

2. ábra

Ebből az is kiolvasható, hogy az

y = a x^{2}

parabola azoknak a pontoknak a mértani helye, amelyek az

F (0, 1 / 4 a)

ponttól (a fókusztól) és az

y = - 1 / 4 a

egyenestől (a vezéregyenestől) egyenlő távolságra vannak. Ha a parabola az

F

fókuszával és a

v

vezéregyenesével van megadva, akkor (11) alapján úgy lehet hozzá a

P

külső pontból érintőt húzni, hogy a

P

körüli,

F

-en átmenő körrel metsszük a

v

egyenest, és vesszük a metszéspont és

F

által meghatározott szakasz felező merőlegesét.

Ennek alapján visszavezethetjük feladatunkat az 1698. feladatra.^{$^{*}$} Legyenek ugyanis a

P

körüli,

F

-en átmenő

k

kör és a

v

egyenes metszéspontjai

M'

és

M''

. Az

F M'

F M''

szakaszok felező merőlegesei közti szög akkor lesz

45^{\circ}

-os, ha

M' P

és

M'' P

merőlegesek egymásra, vagyis a

P M' M''

szög

45^{\circ}

-os, és ugyanennyi

k

és

v

szöge is. Az 1698. feladat megállapítása szerint azoknak a

P

pontoknak a mértani helye, amelyek körül

F

-en átmenő kört rajzolva e kör

v

-t

α = 45^{\circ}

-os szögben metszi, az a hiperbola, amelynek egyik fókusza

F

, centruma az

F V

egyenesnek az a

C

pontja (

V

F

vetülete

v

-n), amelyre

\begin{matrix} F C = (1 + \frac{cos^{2} α}{sin^{2} α}) \cdot F V, \end{matrix}

tehát

α = 45^{\circ}

mellett

C

F

pont

v

-re vonatkozó tükörképe, és a hiperbola valós tengelyének fele‐hossza

\begin{matrix} a = \frac{cos α}{sin^{2} α} F V = \sqrt[]{2} \cdot F V . \end{matrix}

A kapott eredményt szemlélteti a 3. ábra: legyen az

F A C B

négyzet

A B

átlója a

v

egyenesen,

F

-nek

C

-re vonatkozó tükörképe pedig legyen

F_{1}

. Ekkor azoknak a

P

pontoknak a mértani helye, amelyekből az

F

fókuszú,

v

vezéregyenesű parabolához húzott érintők közti szög

45^{\circ}

-os, a

\begin{matrix} | P F - P F_{1} | = 2 \cdot A C \end{matrix}

(12)

tulajdonsággal definiált görbe, vagyis az az

F

F_{1}

fókuszú hiperbola, melyre nézve a valós tengely fele‐hossza

A C

. (Aszimptotái az

A C

B C

egyenesek.)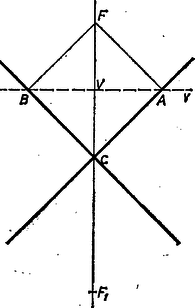

3. ábra

Ha tudjuk, hogy

\begin{matrix} \frac{{(y - c_{2})}^{2}}{a^{2}} - \frac{{(x - c_{1})}^{2}}{b^{2}} = 1 \end{matrix}

annak a hiperbolának az egyenlete, amelyiknek a valós tengelye párhuzamos az

y

tengellyel, valós tengelyének fele

a

, képzetes tengelyének fele

b

és centrumának a koordinátái

(c_{1}, c_{2})

, akkor a vizsgált mértani hely (12) alatti geometriai definíciója (10)-ből is kiolvasható.

^{$^{*}$}Feladatunk a Czapáry E.‐Horvay K.‐Reiman I.‐Dr. Soós P: Geometriai feladatok gyűjteménye c. mű 1. kiadásában (1964) úgy szerepelt 3954. feladatként, hogy a parabola látószöge

45^{\circ}

. Ez hiperbolánknak csak az alsó ágára teljesül, a felső ágon

135^{\circ}

a látószög.

^{$^{*}$}Lásd a megoldását K. M. L. 42 (1971) 52. old.