| Feladat: | F.1747 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Angyal J. , Bálint László , Balog J. , Berkó A. , Blahó Ágnes , Boros Endre , Csetényi A. , Csuhaj László , Dvorák Cecilia , Fazekas I. , Földes T. , Földvári Csongor , Gere Anna , Gerják István , Hosszú F. , Katona Endre , Koch R. , Komornik V. , Molnár József , Nagy S. , Petz D. , Pipek János , Polyák Gábor , Reviczky János , Sashegyi László , Szabó Zoltán , Székely A. , Szendrei Ágnes , Szendrei Mária , Szeredi János , Turán Gy. , Vas Zoltán | ||
| Füzet: | 1973/február, 58 - 60. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Középpontos tükrözés, Négyszögek geometriája, Vektorok lineáris kombinációi, Helyvektorok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1970/december: F.1747 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A négyszögről nincs föltételezve, hogy konvex, ennélfogva lehet konkáv és hurkolt is. Csúcsairól csak azt használhatjuk fel, hogy közülük semelyik három nincs egy egyenesen. Így a feladat első részében az -n átmenő, -vel párhuzamos egyenes nem azonos -vel és nem párhuzamos -vel, tehát létrejön, és ugyanígy is. Vegyük észre, hogy az , betűpár és egyidejűen a , pár tagjait is egymással fölcserélve, az alakzat változatlan marad. 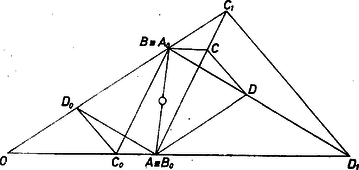 1. ábra Mivel , elegendő azt megmutatni, hogy a feladatban szereplő szakasz -lal párhuzamos. Az négyszögből kiindulva et mint az egyenes és a -on átmenő, -lal párhuzamos egyenes metszéspontját kapjuk meg, hiszen ez az utóbbi az eredeti egyenes, pedig a -n átmenő, -vel párhuzamos egyenes. Hasonlóan a és az -on át -lal párhuzamosan húzott egyenes metszéspontja. Ha a és egyenesek metszik egymást, jelöljük metszéspontjukat -val és az , , , pontoknak az centrumra vonatkozó helyvektorát rendre -lal, -lal, -lal, -lal. Mivel csúcsai között nincs három egy egyenesen, így különbözik a négyszög csúcsaitól, és ezek a helyvektorok nem lehetnek -vektorok. Van tehát olyan és valós szám, hogy Ha és párhuzamosak, vagyis már eleve , akkor azonos -gyel, pedig -gyel, és az állítás nyilvánvalóan igaz. b) A feladat második állításának először a következő részét bizonyítjuk. Ha az egyenes tetszőleges (-tól és -től különböző) pontja, akkor az -n át -gyel és a -n át -gyel párhuzamosan húzott , ill. egyenes a egyenesen (-ben) metszi egymást; mégpedig azzal, hogy az , egyenesek metszéspontját -vel összekötő egyenes párhuzamos -gyel, tehát azonos -vel. Legyen és metszéspontja , alkalmazzuk a feladat első részében bebizonyított tételt az négyszögre, és jelöljük az így , szerepét átvevő pontot -gal, ill. -gal (2. ábra, itt konvex négyszög, és az szakaszon van, ajánljuk az olvasónak, szerkessze újra az ábrát más helyzetű , , , , pontrendszerek esetében). 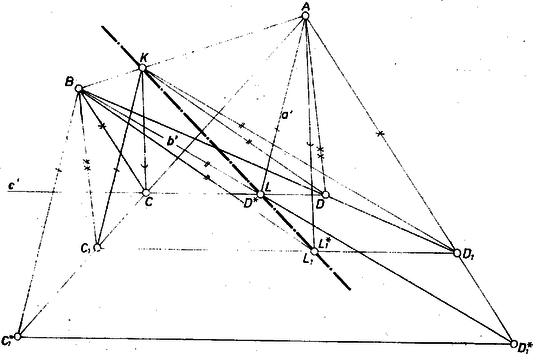 1. ábra Mivel négyszögünk első három szögpontja változatlan. azért az egyenesen van, az -n és szerepére az egyenesnek csak egy pontja nem alkalmas, ti. az, ahol a egyenes átmetszi, ha egyáltalán metszi; akkor nem jön létre. c) A második állítás pontjának a egyenesre illeszkedése most már úgy adódik, hogy az -re kapott eredményt alkalmazzuk az , , , pontnégyesre és az egyenes tetszőleges pontjára. (Az , egyenesek metszéspontja azonban nem szerepelhet -ként.) d) Rátérünk a második állítás hátra levő részének bizonyítására, ti. hogy , és egy egyenes pontjai. Alkalmazzuk az a) eredményt az , , , pont helyén rendre az , , , pontnégyesre és jelöljük -gal azt a pontot, ahol az -n át -vel párhuzamosan húzott egyenes metszi a egyenest. Ezek szerint kapja a tételbeli szerepét, szerepét viszont maga játssza az új négyszögben is. Ekkor pedig Ezzel a bizonyítást befejeztük.
|