Feladat: F.1746 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1971/december, 205 - 207. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Egyéb sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1970/december: F.1746

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az ABCDE egyenlő oldalú konvex ötszög leghosszabb átlója AC. Az AC átló tetszőleges P pontjára az APB és BPC szögek összege 180∘, ezek a szögek tehát csak akkor lehetnek egyszerre 90∘-nál nem nagyobbak, ha mindketten 90∘-osak, azaz P azonos B-nek az AC-n levő F vetületével, ami egyben az AC átló felezőpontja is, hiszen az ABC háromszögben AB=BC. Az ötszög E csúcsa az AC egyenes B-t nem tartalmazó oldalán van, és itt helyezkedik el (B-n kívül) minden további pont, amit megoldásunkban használni fogunk. E továbbá az A középpontú, B-n átmenő k1 körön van, és EC≤AC miatt benne van a C középpontú, A-n átmenő k2 körben. Emiatt E csak a k1 kör kisebbik KG ívén lehet, ahol a K, G pontokat a k2 kör, illetve az AC egyenes metszi ki a k1 körből. Ugyanígy kapjuk, hogy D a C középpontú, B-n átmenő k3 kör LH ívén van, ahol az L, H pontokat az A középpontú, C-n átmenő k4 kör, illetve az AC egyenes metszi ki k3-ból. Jelöljük B-nek F-re vonatkozó tükörképét B'-vel, a k1, k3 körök nyilván B'-n is átmennek (1. ábra).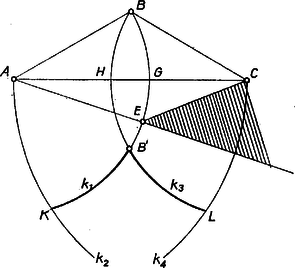

 
 
1. ábra
 

Nem lehet az E pont a k1 kör B'G ívén, hiszen az ötszög konvex volta miatt a D pontnak az AE egyenes C-t tartalmazó oldalán, és az EC egyenes A-t nem tartalmazó oldalán kell lennie, ebben a síkrészben viszont nincs az LH ívnek pontja, ha E a B'G íven van. Tehát E a B'K íven van, és ugyanígy kapjuk, hogy D a B'L íven van. Emiatt az AFE szög nagyobb, mint az AFK szög, vagy ugyanakkora, és kisebb, mint az AFB' szög. Az AFK háromszögben AK=AB>AF, hiszen az ABF háromszög derékszögű, és AB. az átfogója. Emiatt az AFK háromszögben AK-val szemben nagyobb szög van, mint AF-fel szemben, e két szög összege viszont nagyobb 90∘-nál, hiszen FK-val szemben hegyesszög van (ez a szög ugyanis azonos az egyenlő szárú ACK háromszög AK alapján levő egyik szöggel). Tehát az AFK szög 45∘ és 90∘ közé esik és ugyanezt kapjuk a CFD szögre.
Azt kaptuk ezzel, hogy az F pontból az AE, CD oldalak 90∘-nál kisebb szögben látszanak, és e két látószög összege nagyobb 90∘-nál, így pedig a DE oldal is 90∘-nál kisebb szögben látszik F-ből. A feladat állítását ezzel bebizonyítottuk.
 

II. megoldás. Ismét azt bizonyítjuk be, hogy ha az ABCDE ötszög legnagyobb átlója AC, akkor ennek felezőpontjából, F-ből a CD, DE, EA oldalak hegyesszögben látszanak. Mivel AD≤AC, az ACD háromszögben ADC∢≥ACD∢. A CDE háromszög C-nél levő szöge része az ACD szögnek, tehát kisebb annál, a háromszög D-nél levő szöge pedig tartalmazza az ACD szöget, tehát nagyobb annál. Így DCE∢<CDE∢, ezért CE>DE=AE, és így E az AC szakasz felező merőlegesének az A-t tartalmazó oldalán van, amiből következik, hogy az AFE szög hegyesszög. Ugyanígy láthatjuk be, hogy a CFD szög is hegyesszög (2. ábra).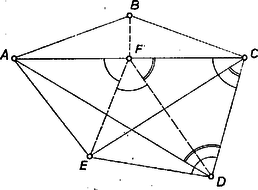
 
 
2. ábra
 

Megmutatjuk, hogy a DEF háromszögben nem ED a legnagyobb oldal. Ha ugyanis EF<ED=AE és FD<ED=CD volna, akkor ‐ a már látott AF<AE, FC<CD miatt ‐ a CFD, DFE, EFA háromszögek mindegyikében az F-fel szemközti oldal volna a legnagyobb, és így F-nél 60∘-osnál nagyobb szög volna. Mivel a három háromszög F-nél levő szögeinek az összege 180∘, ez valóban nem lehet. Tehát a DEF háromszögben nem DE a legnagyobb oldal, így nem F-nél van a legnagyobb szög, vagyis a DFE szög hegyesszög. Ezzel a bizonyítást befejeztük.
 

Megjegyzések. 1. Mindkét megoldásban AC-ről csak az AC≥EC, AC≥AD egyenlőtlenségeket használtuk fel. Amint azt a II. megoldásban láttuk, a DFE szög mindig kisebb 90∘-nál, bármilyen is az átlók nagysága.
2. Megoldásainkban feltételeztük, hogy B nincs az AC oldalon, ebből kaptuk az AB>AF egyenlőtlenséget. Ha megengedjük, hogy egy konvex ötszög két egymáshoz csatlakozó oldala egy egyenesen legyen, feladatunk állítása ekkor is igaz, az általunk adott megoldások is elmondhatók, egy kicsivel több körültekintéssel.
3. Könnyen szerkeszthetünk olyan ötszöget, amilyen a feladatban szerepelt. Ha ugyanis egy hegyesszögű háromszögben a legkisebb oldal nem kisebb a legnagyobb oldal felénél, és a legkisebb oldal hosszával mint szárakkal, a másik két oldal fölé kifelé egyenlő szárú háromszöget rajzolunk, egyenlő oldalú konvex ötszöget kapunk.