Kezdőlap


Feladat:	F.1745	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gurszky Zoltán , Párkány Erzsébet
Füzet:	1972/május, 193 - 195. oldal		PDF \| MathML
Témakör(ök):	Függvény határértéke, Numerikus és grafikus módszerek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1970/december: F.1745

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A leírt alakzat szerkesztésében csak a $G$ metszéspont létrejötte lehet kétséges. A mondott $α < 60^{\circ}$ (és a hallgatólagosan feltett $α > 0^{\circ}$ , enélkül nem lehetne $α \to 60^{\circ}$ ) feltétel mellett, hosszúságegységnek $O A$ -t véve

\begin{matrix} E F = \frac{1}{3} sin 3 α = sin α - \frac{4}{3} {sin}^{3} α < sin α = B K, \end{matrix}

ahol

K

B

pont vetülete

O A

-n (1. ábra felső része), tehát az

A O

és

B F

egyenesek nem párhuzamosak,

G

valóban létrejön, éspedig a

K E

félegyenes

E

-n túli részén.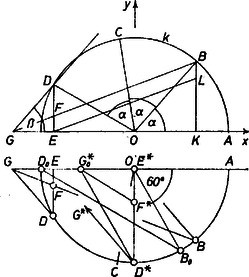

1. ábra

Messe az

E

-n át

B F

-fel párhuzamosan húzott egyenes

B K

-t

L

-ben, és jelöljük az

O G D

szöget

β

-val. Mivel a szerkesztés szerint

β

mindig hegyesszög, elég a tangensét meghatározni:

\begin{matrix} tg β = \frac{E D}{G E} = 3 \frac{E F}{G E} = 3 \frac{K L}{E K} . \end{matrix}

Szerkesztésünk szerint

\begin{matrix} K L = K B - E F = sin α - \frac{1}{3} sin 3 α, E K = cos α - cos 3 α . \end{matrix}

(Az utóbbi megállapításban arra a koordináta-rendszerre gondolunk, amelynek origója

O

, pozitív

x

tengelye az

O A

félegyenes: ebben

K

és

E

abszcisszája

cos α

, ill.

cos 3 α

.) Ezek szerint

\begin{matrix} tg β = 3 \frac{sin α - \frac{1}{3} sin 3 α}{cos α - cos 3 α} . \end{matrix}

(1)

A jobb oldalon álló függvény

α

-nak folytonos függvénye (ahol csak értelmezve van, vagyis mindenütt, ahol

cos α \neq 0

\pm 1

). Tehát

α \to 60^{\circ}

mellett a határértéke egyenlő az

α = 60^{\circ}

melletti értékével, ez pedig

\sqrt[]{3}

.
A

β

szög tangense tehát tart a

60^{\circ}

-os szög tangenséhez, ha

α \to 60^{\circ}

. Mivel

0 < x < 90^{\circ}

mellett a tangens függvény monoton növekedő, tetszőleges

ε

-hoz van olyan

δ

, hogy ha

| 60^{\circ} - x | < ε

-e, akkor

| tg x - \sqrt[]{3} | < δ

. Válasszuk

α

-t olyan közel a

60^{\circ}

-hoz, hogy

| tg β - \sqrt[]{3} | < δ

legyen, akkor

| 60^{\circ} - β | < ε

, tehát

α \to 60^{\circ}

esetén

β \to 60^{\circ}

II. megoldás. Legyen

B

vetülete

A O

-n

K

, tükörképe

A O

-ra

B'

és a

G D

és

B B'

egyenesek metszéspontja

H

(2. ábr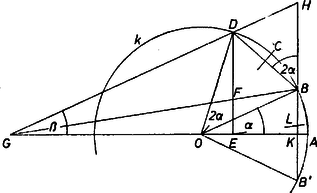a).

2. ábra

Így

B K ∥ D E

, tehát

F E = D E / 3

alapján

B

K H

szakasz

K

-hoz közelebbi harmadoló pontja, és

B H = 2 B K = B B' = B D

, hiszen a

B B' O

és

B D O

egyenlő szárú háromszögek

O

-nál levő szöge

2 α

. Ezért egyrészt a

B D H

háromszög egyenlő szárú, másrészt

B

-nél levő

D B B'

külső szögét a

B O

egyenes felezi (a

D B O

szög is és a

B' B O

szög is pótszöge

α

-nak), tehát

B O

párhuzamos a

D H

alappal. Ennélfogva

B

minden szóba jövő helyzetében

O G D ∢ = A O B ∢ = α

, és ha

α \to 60^{\circ}

akkor

O G D ∢ \to 60^{\circ}

Párkány Erzsébet (Budapest, Berzsenyi D. Gimn., III. o. t. )

Gurszky Zoltán (Vác, Sztáron S. Gimn., III. o. t. )

Megjegyzések. 1. Az

α = β

összefüggést (1) alapján is beláthattuk volna. Ez az összefüggés különben bizonyítható az 1322. gyakorlat^{$^{*}$}, állítása alapján is, feladatunk ebből a gyakorlatból származik.
2. Ha

α \to 60^{\circ}

, akkor

D

pont tart a

k

kör

A

-val átellenes

D_{0}

pontjához, és

D

-vel együtt

D_{0}

-hoz tartanak az

E

F

G

pontok is: a

D E G

háromszög oldalainak a hossza

0

-hoz tart, e háromszög a

D_{0}

pontra ,,zsugorodik össze''. (Tükörkép az 1. ábra alján.) Emiatt a kérdezett

O G D

szög is ,,elvész a szemünk elől'', határhelyzetét nem látjuk, mert a

G D

egyenest meghatározó

2

pont határhelyzete ugyanaz a

D_{0}

pont.
Avégett, hogy ezt megakadályozzuk, rajzoljuk meg az

α \to 60^{\circ}

értékekhez a

D E G

háromszöghöz hasonló

D^{*} E^{*} G^{*}

háromszöget, melyben a

D^{*} E^{*}

szakasz hossza

α

-tól függetlenül egységnyi. Ha

G

tart

D_{0}

-hoz, a

B G

egyenes tart a

B_{0} D_{0}

egyeneshez, ahol

B_{0}

B

pont határhelyzete

α \to 60^{\circ}

esetén, azaz

A O B_{0} ∢ = 60^{\circ}

. Mivel

A D_{0} B_{0} ∢ = A O B_{0} ∢ / 2 = 30^{\circ}

, az

E G F

szög határértéke

30^{\circ}

, azaz rögzített

E^{*}

D^{*}

mellett a

G^{*}

olyan

G_{0}^{*}

ponthoz tart, melyre az

E^{*} F^{*} G_{0}^{*}

háromszögben

E^{*}

-nál derékszög,

G_{0}^{*}

-nál

30^{\circ}

-os szög van (

F^{*}

E^{*} D^{*}

szakasz

E^{*}

-hoz közelebbi harmadolópontja). Tehát az

E^{*} G_{0}^{*} D^{*}

háromszög egy szabályos háromszög fele,

E^{*} G_{0}^{*} D^{*} ∢ = 60^{\circ}

.
Az elmondottakkal csupán szemléltetni kívántuk a feladat állítását, a fenti gondolatmenetben szereplő állításokat nem bizonyítottuk be, még azt sem mondtuk meg, mi ezeknek az állításoknak a pontos jelentése. Megjegyezzük azonban, hogy e vázlatos ,,bizonyítás'' egzakttá tételének nincs akadálya, a határérték fogalma geometriai alakzatokra is kiterjeszthető.

^{$^{*}$}K. M. L. 42 42 (1971) 68. oldal.