Feladat: F.1736 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bacsó Gábor ,  Bánsági Péter ,  Bodnár István ,  Boros Endre ,  Breuer Péter ,  Dauner Henrik ,  Éber Nándor ,  Fazekas István ,  Fazekas Mária ,  Fűzy Csaba ,  Földvári Csongor ,  Gál Péter ,  Horváth László ,  Jáger János ,  Komornik Vilmos ,  Láng István ,  Mester Ferenc ,  Nagy Sándor ,  Pattantyús Péter ,  Petz Dénes ,  Portschy Tamás ,  Revizky János ,  Szász György ,  Szendrei Ágnes ,  Szendrei Mária ,  Szepesi László ,  Tarsó Béla ,  Vályi Géza ,  Vas Zoltán ,  Vogel Anna ,  Zámolyi Ferenc 
Füzet: 1972/november, 134 - 137. oldal  PDF  |  MathML 
Témakör(ök): Határozott integrál, Térfogat, Szabályos sokszögek által határolt testek, Térelemek és részeik, Feladat
Hivatkozás(ok):Feladatok: 1970/október: F.1736

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kérdés kissé szokatlan feltevése ‐ a ,,lehet'' szóval ‐ azt sejteti, hogy a válasz nem egyértelmű, több ilyen test van, és a térfogatuk természetesen más és más. Ezért először azt fogjuk megvizsgálni, melyek azok a testek, amelyekre ráillik a feladatbeli leírás. Külön figyelmet fordítunk azokra a meggondolásokra, amelyekben a konvexséget használjuk fel, mert a versenyzők ezeket a részeket elnagyolták, ,,ösztönösen'' jól alakították ki a testeket, de nem mutatták meg, hogy miért kell ezeknek a testeknek éppen olyanoknak lenniük, mint amilyenek, és így nem bizonyították be, hogy az általuk adott értékek a feladat összes megoldásai. Egy pillantás az 1. ábrára meggyőz arról, hogy ha a konvexséget nem tennénk fel, akkor végtelen sok test felelne meg a követelményeknek.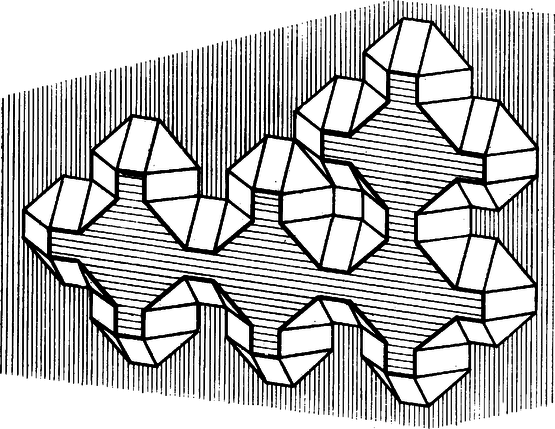

 
 
1. ábra
 

1. Állítsuk képzeletben vízszintesre azokat a párhuzamos síkokat, amelyek a vizsgált T test csúcsait hordozzák, és jelöljük őket S1-gyel és S2-vel. Nevezzük a testnek az S1 és S2 közötti lapjait oldallapoknak, és legyen H a T tetszőleges háromszög alakú oldallapja. Tegyük fel, hogy H-nak S1-ben két csúcsa van, jelöljük ezeket P-vel, Q-val, és legyen R a harmadik csúcs. Jelöljük a H-hoz PR-ben csatlakozó oldallap síkjának S1-gyel alkotott metszésvonalát p-vel. Mivel ez az oldallap téglalap, azért p merőleges PR-re. Hasonlóan legyen q a QR-hez csatlakozó oldallap síkjának és S1-nek a metszésvonala, q merőleges QR-re. Megmutatjuk, hogy p és q a PQ szakasz F felező merőleges síkjára nézve tükrösen helyezkedik el (2. ábra).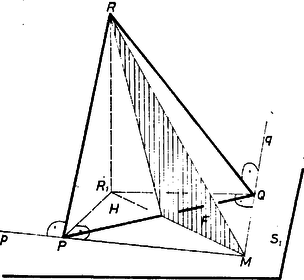
 
 
2. ábra
 

A PR egyenes nem lehet merőleges S1-re, hiszen nem merőleges az S1-beli PQ egyenesre. Így S1-ben csak egy, a P-n átmenő, PR-re merőleges egyenes van. Tükrözzük az S1-ből, H-ból és q-ból álló alakzatot F-re. Ekkor S1 és H önmagába megy át, q képe pedig olyan egyenes, amely átmegy P-n és merőleges PR-re. Mivel ilyen csak egy van, azért q képe csak p lehet, állításunkat ezzel bebizonyítottuk.
Ha H síkja merőleges S1-re, p és q párhuzamosak, és párhuzamos velük a H-hoz PR-ben és QR-ben csatlakozó lapok síkjának r metszésvonala is. Ez az r egyenes benne van S2-ben és a konvexség miatt T-nek az S2-n levő bármely további csúcsa csak r-en lehet rajta. Emiatt T-nek egyetlen további csúcsa van S2-n, legyen ez R1, és legyen P1 és Q1 a PRR1, QRR1 háromszöget téglalappá kiegészítő pont. Ez a PQR alapú; egységnyi magasságú test az egyetlen olyan test, amelyike eleget tesz a feladat követelményeinek, és amelynek van S1-re merőleges háromszög alakú oldallapja. Mivel két csúcsa van S2-n, azért ezt a testet T2-vel jelöljük (3a ábra).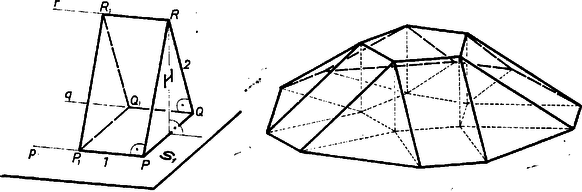
 
 
3a. ábra        3b. ábra
 

Ha H nem merőleges S1-re, akkor az R csúcsának az S1-en levő R1 merőleges vetülete a PQ szakasz felezőpontjától különböző pont. Ismeretes, hogy R1P⊥p és R1Q⊥q, tehát p és q is metszi egymást, a metszéspontjuk, M rajta van az F síkon, és a PR1Q háromszöget deltoiddá egészíti ki. H tehát ,,elhajlik'' M-től, S1-en levő árnyéka a PQ egyenes M-mel ellentétes oldalára esik. Magának a T testnek is ezen az oldalon kell lennie, hiszen konvexitása miatt minden csúcsa a H síkjának ugyanazon az oldalán van, és a H-hoz csatlakozó téglalapok csúcsai nem lehetnek H-nak az M felé eső oldalán, hiszen az MRP és MRQ szögek hegyesszögek, így ezeket a téglalapokat nem lehet az MRP, MRQ síkrészeken elhelyezni. (Ha T nem volna konvex, akkor e téglalapok úgyis elhelyezkedhetnének, hogy egyikük H-nak az M felé eső, másikuk az M-mel ellentétes oldalán van. Ilyen részlet található az 1. ábrán.) Ezzel beláttuk, hogy
a) T-nek a háromszög alakú lapjai a két párhuzamos sík közül ahhoz hajlanak hegyes szögben, amelyiken két csúcsuk van;
b) az egymáshoz csatlakozó háromszögek és téglalapok S1-gyel párhuzamos élei nem alkothatnak hegyes szöget (mert például a 2. ábrán a PR-hez csatlakozó téglalapnak az S1-en levő további csúcsa MP-nek a P-n túli meghosszabbításán van).
c) a háromszög alakú oldallapokhoz csatlakozó téglalapok e háromszögeknek az S1-re merőleges szimmetriasíkjára nézve szimmetrikusan helyezkednek el.
2. Legyen ABCD a T testnek valamely téglalap alakú oldallapja, az A, B csúcsok legyenek S1-en, C és D pedig S2-n. Jelöljük F0-lal a BC és DA szakaszok közös felező merőleges síkját, ebben van benne a BC-hez, illetve DA-hoz csatlakozó háromszög‐lapok E, illetve F csúcsa. Így F0 metszi az S1, S2 síkok közül legalább az egyiket, de akkor S1 és S2 párhuzamos volta miatt a másikat is metszi, és a két metszésvonal párhuzamos. Jelöljük ezeket e1-gyel és e2-vel, F0 és az ABCD lap S síkjának a metszésvonalát e-vel (4. ábr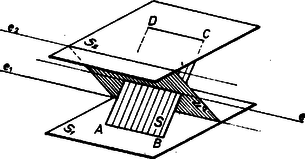a).
 
 
4. ábra
 

Nyilván e is párhuzamos e1-gyel és e2-vel, és e elválasztja egymástól ezt a két egyenest. Emiatt elválasztja egymástól S is az e1 és e2 egyeneseket, tehát T-nek nem lehet e1-en is, és e2-n is csúcsa. Tegyük fel, hogy e2-n nincs csúcsa T-nek, tehát E és F az e1-en van. Az ABEF négyszögben AB párhuzamos EF-fel, BE=AF, és az előző pont szerint az A-beli és a B-beli szög nem lehet hegyesszög. Tehát ABEF szimmetrikus trapéz. Ezzel beláttuk, hogy
a) az ugyanahhoz a téglalaphoz csatlakozó háromszögeknek S1 és S2 közül ugyanabban van a hátralevő csúcsuk;
b) a téglalap alakú oldallapokhoz csatlakozó két‐két háromszög a téglalapnak az S1-re merőleges szimmetriasíkjára nézve tükrösen helyezkedik el.
3. Az előző pont a) megállapításából T-t mintegy körbejárva kapjuk, hogy a háromszög alakú oldallapok mindegyikének S1 és S2 közül ugyanabban van két csúcsa, legyen ez mondjuk S1. Eszerint ha a T test S2-beli csúcsainak a számát n-nel jelöljük, akkor T-nek S1-ben 2n csúcsa van. Könnyű látni, hogy n értéke nem lehet 1, tehát T-nek S1-ben valódi lapja van, jelöljük ezt A2n-nel, és jelöljük T-nek az S2-ben levő részét Fn-nel: ha n=2, akkor Fn csak egy szakasz, különben Fn is lapja T-nek. Az 1. pont c) megállapításából és a 2. pont b) megállapításából következik, hogy A2n szögei egyenlőek. Ebből már könnyen bizonyítható, hogy ha n>2, akkor Fn szabályos n-szög (3b ábra). Az 1. pont a) megállapítása szerint, ha Fn csúcsait S1-re vetítjük, a vetületek benne lesznek A2n-ben.
Jelöljük F területét fn-nel, a téglalap és háromszög alakú oldallapok S1-en levő vetületének a területét tn-nel és hn-nel, a test magasságát λn-nel. Ekkor az S2-től x⋅λn távolságra levő, S2-vel párhuzamos sík a testből
tn(x)=fn+xntn+x2nhn
területű idomot vág ki, tehát a test térfogata
Vn=λn∫01tn(x)dx=λn∫01(fn+xntn+x2nhn)dx==λn(fn+n2⋅tn+n3⋅hn).


Könnyen látható, hogy
fn=n4⋅ctgπn,λn=4-1sin2π/n,tn=1sinπ/n,hn=ctgπ/n,


és hogy, amint az λn fenti alakjából is kiolvasható, n<6. Az n=1, 2, 3, 4, 5 esetekben a feladat követelményeinek eleget tevő testet kapunk, és ezek térfogata
V2=3=1,732,V3=1926=4,478,V4=4+723=7,300,V5=3512+31512=8,693.


Ezzel a megoldást befejeztük.