Kezdőlap


Feladat:	F.1734	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Meződi Judit
Füzet:	1973/január, 16 - 17. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Beírt kör, Hozzáírt körök, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1970/október: F.1734

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszögbe írt kör középpontját $K$ -val, az $A B$ oldalhoz tartozó hozzáírt kör középpontját $O$ -val. Mivel az $A B K$ , $A B O$ háromszögek magassága rendre $r$ és $ϱ$ , azért az $r / ϱ$ hányados egyenlő e két háromszög területének a hányadosával. Jelöljük az $A B C$ háromszög $A$ -nál és $B$ -nél levő szögét a szokásos módon $α$ -val és $β$ -val, akkor az $A B K$ háromszögben az $A B$ alapon levő szögek nagysága $α / 2$ és $β / 2$ , tehát ennek a háromszögnek a területe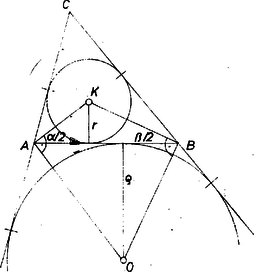

\begin{matrix} t_{A B K} = A B^{2} \frac{sin \frac{α}{2} sin \frac{β}{2}}{2 sin (\frac{α}{2} + \frac{β}{2})} . \end{matrix}

A B O

háromszögben

B A O ∢ = 90^{\circ} - \frac{α}{2}

A B O ∢ = 90^{\circ} - \frac{β}{2}

,
tehát

\begin{matrix} t_{A B O} = A B^{2} \frac{cos \frac{α}{2} cos \frac{β}{2}}{2 sin (\frac{α}{2} + \frac{β}{2})}, \end{matrix}

és ezek szerint

\begin{matrix} \frac{r}{ϱ} = \frac{t_{A B K}}{t_{A B O}} = \frac{sin \frac{α}{2} sin \frac{β}{2}}{cos \frac{α}{2} cos \frac{β}{2}} = tg \frac{α}{2} tg \frac{β}{2} . \end{matrix}

Ez az eredmény természetesen értelemszerűen módosítva érvényes minden háromszögre (bármely háromszögben a beírt kör sugarának és az egyik ‐ alapnak választott ‐ oldalhoz hozzáírt kör sugarának a hányadosa egyenlő az alapon levő szögek felének a tangenséből képzett szorzattal). Így az

A M C

és

B M C

háromszögekben

\begin{matrix} \frac{r_{1}}{ϱ_{1}} = tg \frac{α}{2} tg \frac{A M C ∢}{2}, \frac{r_{2}}{ϱ_{2}} = tg \frac{β}{2} tg \frac{B M C ∢}{2} . \end{matrix}

Mivel az

A M C

és

B M C

szögek egymást

180^{\circ}

-ra egészítik ki, azért

\frac{1}{2} A M C ∢

és

\frac{1}{2} B M C ∢

egymás pótszögei, és így

\begin{matrix} tg \frac{A M C ∢}{2} \cdot tg \frac{B M C ∢}{2} = 1, \end{matrix}

tehát

\frac{r_{1}}{ϱ_{1}}

és

\frac{r_{2}}{ϱ_{2}}

szorzata valóban egyenlő

\frac{r}{ϱ}

-val.

Megjegyzések. 1. A háromszög oldalai, az érintő körök sugarai és a terület között fennálló összefüggések segítségével belátható, hogy a feladat állítása ekvivalens az ún. Stewart-tétellel, mely szerint

\begin{matrix} A C^{2} \cdot M B + B C^{2} \cdot A M = (M C^{2} + A M \cdot M B) A B . \end{matrix}

Az ehhez szükséges algebrai átalakítások azonban nem érik meg a fáradságot, mert a Stewart-tételt körülbelül ugyanolyan nehéz bizonyítani ‐ ha nem nehezebb mint a feladatban szereplő összefüggést.
2. A feladat állításából triviálisan következik az alábbi általánosítás. Ha

A_{0}, A_{1}, ..., A_{k}

egy egyenes egymást követő pontjai,

C

az egyenesen kívül levő pont,

r_{i}

és

ϱ_{i}

A_{i - 1} A_{i} C

háromszögbe, ill. az

A_{i - 1} A_{i}

oldalhoz írt kör sugara

(i - 1, 2, ..., k)

r

és

ϱ

A_{0} A_{k} C

háromszögbe, ill. az

A_{0} A_{k}

oldalhoz írt kör sugara, akkor

\begin{matrix} \frac{r_{1}}{ϱ_{1}} \cdot \frac{r_{2}}{ϱ_{2}} \cdot ... \cdot \frac{r_{k}}{ϱ_{k}} = \frac{r}{ϱ} . \end{matrix}