Feladat: F.1728 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Angyal József 
Füzet: 1972/január, 4 - 6. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Oldalfelező merőleges, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):Feladatok: 1970/szeptember: F.1728

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ABC háromszög köré írt k kör P pontból vett látószögének szárai a P-ből k-hoz húzott érintők, és k minden pontja benne van az érintők által meghatározott szögtartományban, beleértve ennek határait. Így a BC húr P-ből vett látószögének szárai is benne vannak a szögtartományban, ezért az utóbbi látószög csak úgy lehet egyenlő az előbbivel, ha egyben azonos is vele. Eszerint a PB egyenes B-ben, PC pedig C-ben érinti k-t, más szóval P a k-hoz B-ben és C-ben húzott érintők metszéspontja.
A feladat létező P pontról beszél, tehát BC nem átmérője k-nek, és így a BAC szög nem derékszög. Eszerint az AC egyenes nem párhuzamos az AB oldalszakasz f felező merőlegesével, ezeknek a feladatban említett közös pontja szintén létezik, jelöljük E-vel. Az állítás szerint E-n harmadikként átmegy a P-n át AB-vel párhuzamosan húzott egyenes is. Alább ezt azzal bizonyítjuk, hogy az E-t P-vel összekötő egyenes párhuzamos AB-vel. (EP is meghatározott egyenes, nem lehet E a P-vel azonos, hiszen P a BC felező merőlegesén van, aminek f-fel közös pontja csak O, a kör középpontja, P viszont külső pont.)
Az állítás nyilvánvaló abban az esetben, ha CA=CB, amikor E azonos C-vel. Ezt a továbbiakban már nem tekintjük. Megmutatjuk, hogy minden más esetben E rajta van a BCP háromszög köré írt körön, éspedig azzal, hogy a BC-nek vagy az E-ből vett látószöge, vagy pedig ennek kiegészítő szöge egyenlő a P-ből vett látószögével, és egyidejűleg E vagy ugyanazon a partján van BC-nek, mint P, vagy a másik partján.
Valóban, ha A a nagyobbik BC íven van, azaz BAC∢<90∘, akkor E az AC félegyenesen van, az EAB egyenlő szárú háromszögnek A-nál ‐ vagyis az alapján ‐ levő szöge azonos a CAB szöggel, ez pedig egyenlő a szárai közti CB íven nyugvó (érintő szárú) PCB szöggel, a PCB egyenlő szárú háromszög alapján levő szöggel. Ezért a két háromszög alapjával szemben fekvő szögek is egyenlők: AEB∢=CPB∢. Továbbá az AEB szög aszerint azonos a CEB szöggel, ill. kiegészítő szöge neki, hogy E a BC egyenesnek a P-t tartalmazó partján van-e, ill. a másik partján (1. ábra a), ill. b) része).

 
 
1a. ábra
 
 
1b. ábra
 

Mármost a BCP háromszög köré írt kör azonos az OP szakasz fölé írt Thalész körrel, ezért OEP∢=OCP∢, derékszög, s mivel AB is merőleges OE-re, azért PE∥AB, ezt akartuk bizonyítani. ‐ Bizonyításunk utolsó lépése nem érvényes arra az esetre, ha E azonos O-val, ami akkor áll be, ha AC átmegy O-n, vagyis a k-nak átmérője, mert így a körön bárhol véve B-t, AB felező merőlegese mindig O-ban metszi AC-t. (1. ábra c) része).
 
 
1c. ábra
 

Ebben az esetben BC merőleges AB-re is, OP-re, azaz EP-re is, tehát e két egyenes párhuzamos, az állítás ekkor is érvényes.
Ha pedig A a rövidebbik BC ívén van k-nak (2. ábra), akkor a CA félegyenes a PCB szögtartományban halad, tehát szétválasztja a B, P pontokat, a BA félegyenes pedig a PBC szögtartományban, így BP szétválasztja A-t és E-t, ezért E a CA-nak A-n túli meghosszabbításán van.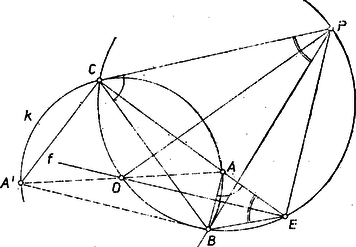
 
 
2. ábra
 

Ekkor fenti meggondolásunk csupán ezzel a kezdőrésszel egészítendő ki: az EAB∢ ‐ mint a CAB háromszög külső szöge ‐ egyenlő a CA'B∢-gel, ahol A' a k-nak A-val átellenes pontja, és ezért egyenlő a PCB érintő szárú kerületi szöggel.
Ezzel a bizonyítást befejeztük.
 

Angyal József (Budapest, Berzsenyi D. Gimn. IV. o. t.)

dolgozata alapján, kiegészítésekkel, egyszerűsítésekkel