Kezdőlap


Feladat:	F.1723	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Angyal József , Skopál József
Füzet:	1971/április, 153 - 154. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):	Feladatok: 1970/május: F.1723

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $k_{j}$ és $e_{j}$ érintkezési pontja $E'_{j}$ , továbbá $k_{j}$ sugara $r_{j}$ $(j = 1$ , $2)$ . Mivel az $E_{j}$ pontokat egy, az $O$ -ból induló félegyenes metszette ki az $e_{j}$ érintőkből, azért $O$ az $E_{1} E_{2}$ szakasz valamelyik meghosszabbításán van rajta. Ezt ‐ mivel $e_{1}$ és $e_{2}$ párhuzamosak ‐ így is mondhatjuk: $O$ nincs közte $e_{1}$ -nek és $e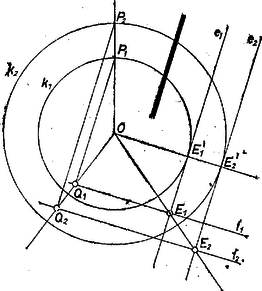_{2}$ -nek.

Választhatjuk úgy az indexelést, hogy

0 < r_{1} < r_{2}

(hiszen az

r_{1} = r_{2}

eset nyilvánvalóan semmitmondó), így

e_{1}

elválasztja

O

-t és

e_{2}

-t. Az

e_{1} ∥ e_{2}

tényből az is következik, hogy

O

E'_{1}

és

E'_{2}

egy egyenesen vannak, éspedig

E'_{1}

O E'_{2}

szakaszon. Ezek szerint az

O E_{1}

O E'_{1}

félegyenesek között hegyesszög van, és

\begin{matrix} O E_{1} : O E_{2} = O E'_{1} : O E'_{2} = r_{1} : r_{2} = O P_{1} : O P_{2}, \end{matrix}

így az

E_{j} P_{j}

szakaszok egymás képei az

O

középpontú,

r_{1} : r_{2}

arányú hasonlósági transzformációban, tehát párhuzamosak egymással.
Másrészt a

Q_{j}

pontokat előállító

f_{j}

, valamint

P_{j} Q_{j}

egyenespárok szerkesztésüknél fogva páronként párhuzamosak, ezért ezek is és

Q_{1}

és

Q_{2}

is egymás képei a mondott transzformációban, tehát az utóbbiak összekötő egyenese átmegy

O

-n. Ezt kellett bizonyítanunk.
Meggondolásunk akkor is érvényes, ha a

P_{j}

pontokat kimetsző félegyenes az

E_{j}

-ket kimetsző félegyenesnek

180^{\circ}

-kal elfordított képe az

O

körül. Ha pedig az

O P_{1}

párhuzamos

i

-vel, akkor az állítás semmitmondóan igaz.

Skopál István (Budapest, Kölcsey F. Gimn., IV. o. t.)

Angyal József (Budapest, Berzsenyi D. Gimn., III. o. t.)