Feladat: F.1722 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Ferró József ,  Garay Barnabás ,  Gáspár Gyula ,  Kiss Ipoly ,  Komornik Vilmos ,  Poór Zsolt ,  Reviczky János ,  Selényi Péter ,  Simon Júlia ,  Szendrei Mária 
Füzet: 1972/február, 59 - 62. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1970/május: F.1722

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A C0C1C2...C17=S18 szabályos 18-szöget O középpontja körül 360∘:18=20∘-kal elfordítva minden csúcs a rá következőbe megy át, minden átló egy átló helyére jut, és ugyanez áll a kívánt tulajdonságú metszéspontokra is. Ezért elég az OC0C1=H egyenlő szárú háromszög belsejében és ennek C0O szárán ‐ végpontjait azonban a feladat szövege alapján kizárva ‐ megkeresni azokat a pontokat, amelyeken legalább 4 átló megy át; az ilyen pontok számának 18-szorosa lesz a válasz a feladat kérdésére.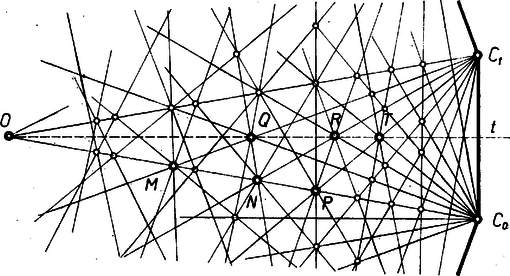

 
 
1. ábra
 

Gondos ábrát készítve a H-n áthaladó átlókról (1. ábra), úgy látjuk, hogy a követelmény szempontjából csak a C0O sugár M, N, P pontjai és a háromszög t tengelyének Q, R, T pontjai jönnek szóba. Megmutatjuk, hogy az előbbi három ponton 5‐5, az utóbbi hármon 4‐4 átló megy át. (Az ábra nem kivonatként készült egy teljes ábrából, hanem számítások alapján.)
Az M-en átmenni látszó átlók közül a C1C11 és C17C7, valamint a C3C14 és C15C4 pár tagjai (2. ábra) mindenesetre C0O-n metszik egymást, hiszen erre, mint S18 tengelyére nézve egymás tükörképei (Ci -nek tükörképe C18-i, ha 0< <i<18), ezért elég belátnunk, hogy C1C11 és C17C7-nek M1 metszéspontja azonos C1C11-nek és C3C14-nek M2 metszéspontjával. Valóban, C17C1C11∢=C1C17C7∢=60∘ mint az S18 köré írt k kör kerületének 1/3 részét kitevő íven nyugvó kerületi szögek, ezért C1C17M1 egyenlő oldalú háromszög, így C1M1=C1C17=C1C3, másrészt ugyancsak kerületi szögekként C3C1M2∢=C3C1C11∢=80∘, C1C3M2∢=50∘, ezért C1M2C3∢=50∘, C1C3M2 egyenlő szárú háromszög, C1M2=C1C3=C1M1. Eszerint M2 azonos M1-gyel, meglátásunk helyes, M a követelménynek megfelelő pont.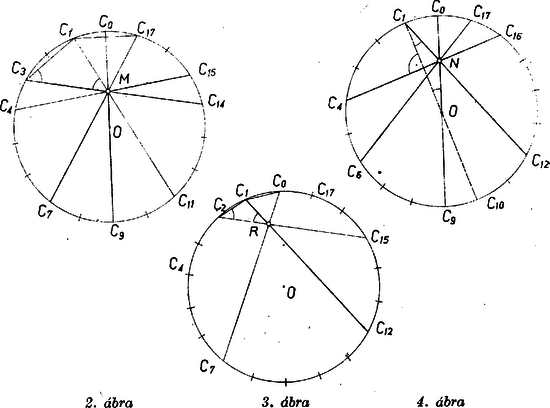
 

 

Hasonlóan R esetében (3. ábra) C1C12-nek és C0C7-nek a C0C1 oldalszakasz felező merőlegesén levő R1 metszéspontja egyenlő oldalú háromszöget alkot C0-lal és C1-gyel, másrészt C1C12-nek és C2C15-nck R2 metszéspontja (100∘ szárszögű) egyenlő szárú háromszöget alkot C1-gyel és C2 vel. Így C1R2=C1C2=C1C0=C1R1, tehát R2 azonos R1-gyel, és itt megy át a szimmetria folytán C17C4 is, R-ben tehát 4 átló metszi egymást.
 

Az N és P, valamint Q és T pontok esetében azt használjuk fel bizonyításunkban, hogy a rajtuk átmenni látszó átlók közül kettő‐kettő S18-ról ennek 6 oldalát metszi le, így a hozzá tartozó középponti szög 120∘, és mindegyik ilyen átló egy‐egy OCi(=CiCi±9) sugár felező merőlegese, tehát rá vonatkozóan O és Ci egymás tükrös párja.
 

N-et a C0O=C0C9 szimmetriatengely és a C4C16 átló metszéspontjának tekintve (4. ábra) S18 szimmetriája alapján itt átmegy C14C2 is; másrészt O-nak C4C16-ra való tükörképe C1, és ezt N-nel összekötve a C1C12 átlót kapjuk, mert így NC1O∢=NOC1∢=C0OC1∢=20∘=C12C1C10∢=C12C1O∢, hiszen C0 és C12, a C1C10 átmérővel kettévágott síknak ugyanazon a felén vannak, tehát ezen van N is. Így pedig C1C12-nek C0O-ra tükrös párja, C17C6 is átmegy N-en.
 

Ugyanígy, P-t OC0 és C5C17 közös pontjának tekintve, átmegy rajta C2C15, mert O tükörképe C5C17-re C2, és PC2O∢=POC2∢=C0OC2∢=40∘; a C2-n átmenő átmérő C2C11, és ettől 40∘-kal van elfordulva a 11+4=15 indexű csúcsba menő C2C15 egyenes. Továbbá átmegy P-n C5C17-nek és C2C15-nek C0C9-re való C13C1, ill. C16C3 tükörképe. Ezek szerint az N, P pontokon 5‐5 átló megy át.
 

Q-t C4C16 és a t tengely metszéspontjának tekintve, átmegy rajta C4C16-nak t-re való C15C3 tükörképe (Ci-nek t-re való tükörképe C19-i, ha i≧2) és t-nek C4C16-ra való tükörképe, ez pedig ugyancsak átlója S18-nak, mert O képe C1 és QC1O∢=QOC1∢=10∘=C11C1C10∢=C11C1O∢, tehát a kép a C1C11 átló; végül átmegy Q-n C1C11-nek t-re való C0C8 tükörképe, tehát Q-n 4 átló megy át. Ugyanez hasonlóan bizonyítható T-re, mint t és a C0C6 átló metszéspontjára, s a rajta átmenő további 3 átló: C1C13, C3C17 és C16C2.
 

Mindezek szerint a követelményt S18-han 18⋅6=108 pont teljesíti.
 

Kiss Ipoly (Budapest, Berzsenyi D. Gimnázium)

Reviczky János (Budapest, I. István Gimnázium)
 

II. megoldás. Az I. megoldásban megsejtett csomópontok valódi voltát számítással igazoljuk. Legyen az O közepű egységkör egy húrjának látószöge 2φ, a húr felezőpontja F, és egy, az O-ból kiinduló x félegyenesnek OF-fel bezárt szöge λ, a húron levő pontja X (5. ábra), ekkor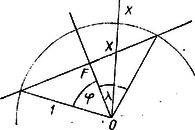
OX=OFcosλ=cosφcosλ(<1,haλ<φ)
x-ként előbb OC0-t, majd a t tengelyt veszszük, továbbá k-ként az egységkört, húrként pedig az M, ..., T-ben szóba jövő kétféle (C0C9 nél kisebb) átlóból egyet‐egyet.
 
 
5. ábra
 

Az egyes csomópontok akkor és csak akkor léteznek, ha a táblázatban a ★ jelek helyére írhatunk egyenlőségi jelet. A két‐két hányados (arány) egyenlősége helyett a közös nevezőre hozott alakok számlálójában álló szorzatokat fogjuk vizsgálni.
 

A φ érték, valamint OF-nek irányszöge könnyen megállapítható OCi-nek OC0-tól mért i⋅20∘ irányszögéből, az utóbbi egyszersmind λ értéke, ha x-nek OC0-t vesszük x≡t esetén pedig ennél 10∘-kal kisebb.
Mármost a kérdéses szorzatok egyenlősége mindhárom esetpárban (a párok M és Q, továbbá N és R, végül P és T) a
cos60∘cos2z=12sin(90∘-2z)=sin(45∘-z)=cos(45∘-z)=cos(45∘+z)cos(45∘-z)
azonosságból következik, 2z-t rendre 70∘-nak, 50∘-nak, ill. 10∘-nak véve. Ezek szerint az x helyére mindenütt beírható az egyenlőség, a bizonyítást befejeztük.
 

φλA kérdéses  OXHelyette vizsgálhatókifejezés|M  C15C4C17C770∘80∘10∘60∘cos70∘cos10∘⋆cos80∘cos60∘cos70∘cos60∘*cos80∘cos10∘|N  C16C4C17C660∘70∘20∘50∘cos60∘cos20∘⋆cos70∘cos50∘cos60∘cos50∘*cos70∘cos20∘|P  C16C3C17C550∘60∘   10∘40∘cos50∘cos10∘⋆cos60∘cos40∘cos50∘cos40∘*cos60∘cos10∘|Q  C16C4C0C860∘80∘   10∘70∘mint  M-nél|R  C17C4C0C750∘70∘   20∘60∘mint  N-nél|T  C17C3C0C640∘60∘   10∘50∘mint  P-nél