|
| Feladat: |
F.1718 |
Korcsoport: 16-17 |
Nehézségi fok: nehéz |
| Megoldó(k): |
Angyal J. , Barbarits A. , Boros E. , Eller J. , Fazekas Gábor , Fazekas István , Ferró J. , Földes T. , Garay B. , Gáspár Gy. , Glódy A. , Győry Gy. , Hadik R. , Hermann T. , Hollósy G. , Horváthy P. , Juhász Júlia , Kacsuk P. , Kérchy L. , Kertész Á. , Komornik V. , Kuhár J. , Lévai G. , Major T. , Maróti Gy. , Papp Gábor , Pataki B. , Reviczky J. , Schmidt F. , Selényi P. , Simon Júlia , Szabó György , Szendrei Ágnes , Szendrei Mária , Szente J. , Takács Helga , Turán Gy. , Török I. , Vajnági A. , Varsányi I. , Vogel Anna , Zulauf Erzsébet |
| Füzet: |
1970/november,
131 - 135. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Tetraéderek, Feladat |
| Hivatkozás(ok): | Feladatok: 1970/április: F.1718 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. a) A esetben válasszuk úgy az tetraéder betűzését, hogy az egységnyi él legyen, és a él felezőpontját jelöljük -vel. Az háromszög minden oldala egységnyi, ezért , és hasonlóan . 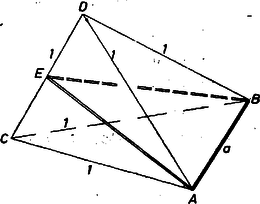 1. ábra
Az háromszögben , vagyis (1. ábra) (1) ezek szerint szükséges feltétele a szóban forgó tetraéder létezésének. Megmutatjuk, hogy ez a feltétel elégséges is. Ha ugyanis (1) teljesül, van olyan egyenlő szárú háromszög, melynek alapja , és szárai egységnyiek. Ennek a csúcsában a síkjára merőleges egyenesre mindkét irányban egységet felmérve a kapott végpontok az alap két végpontjával együtt a kívánt tulajdonságú tetraédert határozzák meg.
b) mellett két esetet kell megkülönböztetnünk aszerint, hogy a két egységnyi él csatlakozik-e egymáshoz vagy nem. Ha csatlakoznak, közös végpontjuk legyen , másik két végpontjuk és , a tetraéder negyedik csúcsa és felezőpontja (2. ábra). 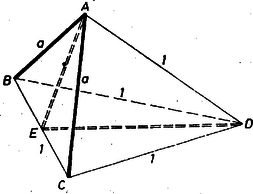 2. ábra
Mivel egyenlő szárú háromszög, merőleges -re és az háromszögben Az háromszögben
Ezek alapján ebben az esetben a tetraéder létezésének szükséges feltétele.
Ha (2') teljesül, az egységnyi alapú és egységnyi szárú háromszög magasságából és az , oldalakból háromszög szerkeszthető, ennek csúcsát az háromszög síkjára -ben emelt merőleges síkban elhelyezve, a kívánt tulajdonságú tetraédert kapunk.
Ha a két egységnyi él kitérő egymáshoz képest, legyen ez a két él az és , és felezőpontjuk legyen , ill. (3. ábra). 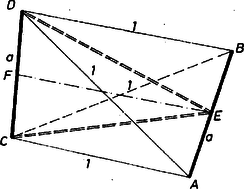 3. ábra
Mivel az és háromszögek egyenlő szárúak, azért merőleges -re is, -re is, tehát merőleges a háromszög síkjára, és hasonlóan merőleges az háromszög síkjára. Az egymáshoz csatlakozó , , szakaszokra a térbeli Pitagorasz-tételt felírva kapjuk, hogy
Ha (2'') teljesül, az hosszúságú szakaszra a végpontjaiban rá, valamint egymásra merőlegesen felvéve az egységnyi , szakaszokat úgy, hogy felezőpontjuk , ill. legyen, a kapott tetraéder , , , éle a fenti meggondolás alapján egységnyi lesz, tehát (2'') egyszerre szükséges és elegendő feltétele is a kívánt tetraéder létezésének, a vizsgált él-elrendezés mellett.
E két esetet összefoglalva kimondhatjuk, hogy akkor és csakis akkor van olyan tetraéder, melynek négy éle egységnyi és két éle egységnyi, ha a (2'), (2'') feltételek közül legalább az egyiknek eleget tesz, vagyis ha
c) Egy tetraéder élei közül többféleképpen választhatunk ki hármat, a legegyszerűbb esetben ezek az egyik lap élei. Legyen ez a lap az , a negyedik csúcs, és az lap centruma (4. ábra). 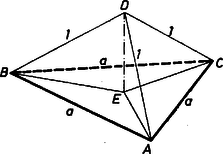 4. ábra
Az háromszög szabályos, így a tér azon pontjainak mértani helye, melyek a három csúcstól egyenlő távolságra vannak, a háromszög síkjára -ben emelt merőleges. Ezen van a tetraéder csúcsa is, hiszen . Az szakasz vetülete e síkon , emiatt . Az oldalú szabályos háromszög köré írható kör sugara , tehát csak akkor teljesülhet, ha
Ha pedig (3') teljesül, az oldalú szabályos háromszög centrumában emelt merőlegesre felmérve a szakaszt, a kapott tetraéder oldalélei egységnyiek lesznek, (3') tehát elégséges is ahhoz, hogy legyen olyan tetraéder, melynek három éle egy egységnyi és három éle egységnyi.
Ennek az elrendezésnek komplementere az, amelyben a db egységnyi oldal helyezkedik el egy lapon (5. ábra). 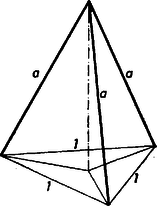 5. ábra
Ezt az esetet azonban már nem kell részletesen tárgyalnunk, fenti eredményünk ezt is magában foglalja. Ha ugyanis az előbb azt vizsgáltuk volna, hogy milyen összefüggés áll fenn a alapélű és oldalélű tetraéder két meghatározó adata között, akkor fenti meggondolásunkkal a egyenlőtlenséget kaptuk volna, (3') ennek a , esete.
Ha viszont és , akkor fenti egyenlőtlenségünkből a komplementer elrendezésre vonatkozó szükséges és elegendő feltételt kapjuk.
A kívánt tulajdonságú tetraéder létezéséhez tehát elégséges, ha vagy (3')-nak vagy (3'')-nak eleget tesz. Mivel tetszőleges valós szám eleget tesz e két egyenlőtlenség valamelyikének, ilyen tulajdonságú tetraéder tetszőleges mellett létezik, csak a feladatban is kimondott feltételnek kell teljesülnie.
d) Felesleges részletesen megvizsgálnunk a esetet, hiszen legutóbbi eljárásunkkal ez visszavezethető a esetre (előbb a esetben mondottakat általánosítva arra az esetre, amikor két él egységnyi, és négy él egységnyi, majd a , adatokra kapott egyenlőtlenségbe a , értékeket helyettesítve). Azt kapjuk így, hogy mellett a keresett szükséges és elégséges feltétel
e) Végül a esetre vonatkozó feltétel a eset alapján hasonlóan Ezzel az összes esetet megvizsgáltuk, feladátunk megoldását tehát befejeztük.
Megjegyzések. 1. mellett van még egy elrendezési lehetőség, amelynek vizsgálata nem szerepel megoldásunkban: amikor az egyenlő hosszúságú élek egymás után csatlakoznak, de nem záródnak háromszöggé. Belátható, hogy ilyen tetraéder akkor és csak akkor létezik, ha ennek elemzésére azonban nem volt szükség, hiszen a másik két elrendezés közül legalább az egyik bármely mellett megvalósítható. (Ennek az esetnek az önálló vizsgálata volt az 1646. feladat.)
2. Elég sok dolgozat a eset kétféle elrendezése nyomán mintegy ,,kisiklott'', tovább már az összeállítási lehetőségek számát tekintette fő kérdésnek, ill. a megoldás okvetlenül végrehajtandó lépésének. Ez terjengősségre vezetett és hibalehetőségek léptek föl. Az persze kissé szerencse dolga, hogy valaki esetén a szabályos gúlák esetét veszi-e előbbre, s így rájön, hogy további él-elrendezés figyelembevétele fölösleges, az 1646. feladatbeli vizsgálatra itt nincs szükség. Erre azonban akkor is rá kell jönni, ha a kevésbé szerencsés sorrendben vesszük a lehetőségeket, és az 1646. feladatbeli él-elrendezés és a kétféle szabályos gúla adta föltételeket egybevetjük. Ekkor ‐ rájőve az előkészítés egy részének fölösleges voltára ‐ a végleges leírásban el kell hagyni azt a részletet, bármilyen tetszetős is az.
Lásd ezen számban, 109. o. |
|
 PDF |
PDF |  MathML
MathML 



