Kezdőlap


Feladat:	F.1716	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Barbarits A. , Bognár B. , Földes T. , Garay G. , Gáspár Gy. , Hollósy G. , Kacsuk P. , Kiss Ipoly , Maróti Gy. , Pataki B. , Reviczky J. , Selényi Péter , Simon Júlia , Szabó Gy. , Szendrei Ágnes , Szendrei Mária , Szepesi L. , Vajnági A.
Füzet:	1972/január, 1 - 4. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Hiperbola egyenlete, Kúpszeletek érintői, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1970/április: F.1716

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Helyezzünk ábránkra koordináta‐rendszert úgy, hogy origója az $A B C D = N$ négyzet középpontjába essék és $A$ koordinátái ( $1; - 1$ ) legyenek (az ábra $α$ és $β$ része).

1a. ábra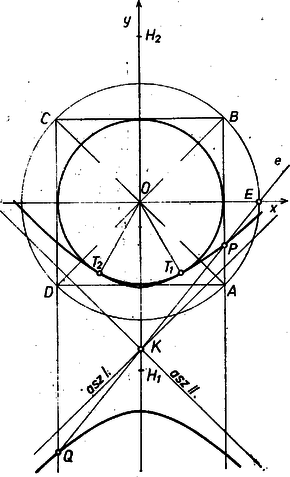

1b. ábra

Így

B (1; 1)

C (- 1; 1)

D (- 1; - 1)

, továbbá az

E

pont (

\sqrt[]{2}; 0)

, az

E

-n átmenő és

A B

-t metsző tetszőleges

e

egyenes egyenlete

\begin{matrix} y = m (x - \sqrt[]{2}), \end{matrix}

(1)

ahol

m

bármely valós szám. Minthogy azonban

E

rajta van

N

-nek

A B

-re merőleges szimmetriatengelyén, az

x

tengelyen, és így az

m

iránytangensű

e

-ből kiindulva készített ábrát az

x

tengelyre tükrözve a (

- m

)-hez tartozó ábrát kapjuk, azért elég az

m \geq 0

értékeket tekinteni.

A kérdéses

P

pont (1)-ből: (1;

m - m \sqrt[]{2}

), hiszen

A B

egyenlete

x = 1

, viszont

Q

abszcisszája

- 1

, mert

C D

egyenlete

x = - 1

; így a hiperbola

K

középpontjának abszcisszája a felezés folytán 0, s mivel

K

is rajta van

e

-n, ezért

K (0; - m \sqrt[]{2})

. A két aszimptota iránytangense

N

átlóiból

+ 1

és

- 1

, tehát egyenletük (mivel átmennek

K

-n):

(2)

y = x - m \sqrt[]{2}

, (2

'

)

y = - x - m \sqrt[]{2}

A hiperbola valós és képzetes (szimmetria) tengelye felezi az aszimptoták közti szögeket, tehát egyikük maga az

y

tengely, a másik párhuzamos az

x

tengellyel. Ebben a tengelyállásban az aszimptoták iránytangense általában

\pm b / a

, ahol

b

és

a

a hiperbola

{(x / a)}^{2} - {(y / b)}^{2} = 1

középponti egyenletének állandói,^{$^{*}$} esetünkben tehát

b / a = 1

b = a

. A hiperbola egyenletének felírásához éppen azt kell még megállapítanunk, hogy szimmetriatengelyei közül melyik a valós tengely, ti. az, amely a két aszimptota által létrehozott 4 síknegyed közül a

P

hiperbolapontot tartalmazó negyedben halad. [Maga

P

nem lehet két síknegyed határán, egyik aszimptotán sem, mert hiperbolának nincs pontja (a végesben) az aszimptotáján, tehát

P

koordinátáival nem teljesülhet (2), emiatt az

m = 1

értéket figyelmen kívül kell hagynunk.] Behelyettesítve

P

koordinátáit (2) bal és jobb oldalának különbségébe:

\begin{matrix} m (1 - \sqrt[]{2}) - (1 - m \sqrt[]{2}) = m - 1, \end{matrix}

és ez

m < 1

esetén negatív,

P

az első aszimptota alatt van. S mivel a második aszimptotának mindenesetre fölötte van ‐ a hasonló különbség (2

'

)-ből

m + 1 > 0

, azért ekkor az

y

tengely a hiperbolának képzetes tengelye (lásd

α

).
Az

m > 1

esetben viszont pozitív a fenti különbség,

P

mindkét aszimptotának fölötte van, az

y

tengely a valós tengely szerepét kapja (lásd

β

). Így a hiperbola egyenlete

\begin{matrix} m < 1 esetén \frac{x^{2}}{a^{2}} - \frac{{(y + m \sqrt[]{2})}^{2}}{a^{2}} = 1 alakú, \\ m > 1 esetén - \frac{x^{2}}{a^{2}} + \frac{{(y + m \sqrt[]{2})}^{2}}{a^{2}} = 1 alakú, \end{matrix}

és

a

értékét abból kapjuk, hogy

P

koordinátái kielégítik az egyenletet:

\begin{matrix} a^{2} = {\begin{matrix} 1 - m^{2}, ha m < 1, \\ - 1 + m^{2}, ha m > 1. \end{matrix} \end{matrix}

Ezek szerint az egyenlet a két esetben közösen:

\begin{matrix} x^{2} - {(y + m \sqrt[]{2})}^{2} = 1 - m^{2} . \end{matrix}

(3)

2. Az

N

-be beírt kör egyenlete nyilvánvalóan

\begin{matrix} x^{2} + y^{2} = 1. \end{matrix}

(4)

3. Két görbére akkor mondjuk, hogy érintik egymást, ha van közös pontjuk és abban közös az érintőjük. Esetünkben a közös pont koordinátáit a (3), (4) egyenletrendszer valós megoldásai adják. (4)-ből (3)-at kivonva, majd 0-ra redukálva

\begin{matrix} 2 y^{2} + 2 \sqrt[]{2} m y + m^{2} = 2 {(y + \frac{m}{\sqrt[]{2}})}^{2} = 0, \end{matrix}

(5)

eszerint közös pontjuk ordinátája csak

\begin{matrix} y_{1} = - \frac{m}{\sqrt[]{2}} \end{matrix}

lehet, és ehhez (3) és (4) bármelyikéből

\begin{matrix} x_{1} = \sqrt[]{1 - \frac{m^{2}}{2}}, x_{2} = - x_{1}, \end{matrix}

ami csak akkor valós, ha

m^{2} \leq 2

. A hiperbolának és a körnek tehát két közös pontja van:

T_{1} (x_{1}, y_{1})

és

T_{2} (- x_{1}, y_{1})

, ha

0 < m < \sqrt[]{2}

, de

m \neq 1

, továbbá egyetlen közös pontjuk

T (0; - 1)

, ha

m = \sqrt[]{2}

.
Vegyük észre, hogy

y_{1}

fele a

K

középpont ordinátájának, eszerint a közös pontok (ill. pont) az

O K

szakasz felező merőlegesén vannak.
A közös pontbeli érintők helyett a normálisokról mutatjuk meg, hogy azonosak, aminek feltétele az iránytényezők egyenlősége. Könnyű belátni a már idézett

^{1}

összefüggések alapján, hogy ha a hiperbola középpontja (

u

v

) és tengelyei párhuzamosak a koordinátatengelyekkel, akkor az (

x_{1}

y_{1}

) pontjában húzott érintő egyenlete a valós tengely állása szerint:

\begin{matrix} \frac{(x_{1} - u) (x - u)}{a^{2}} - \frac{(y_{1} - v) (y - v)}{b^{2}} = \pm 1. \end{matrix}

Ezt alkalmazva

b^{2} = a^{2}

u = 0

és

v = 2 y_{1}

esetében az érintő, majd a rá merőleges normális iránytényezője

\begin{matrix} (\frac{x_{1} - u}{a^{2}}) : (\frac{y_{1} - v}{b^{2}}) = \frac{x_{1}}{y_{1} - v} = - \frac{x_{1}}{y_{1}}, ill. \frac{y_{1}}{x_{1}} . \end{matrix}

Az utóbbi viszont egyszersmind a kör normálisának,

O T_{1}

-nek iránytényezője, a

T_{1}

pontban, hacsak

x_{1} \neq 0

, hiszen (

x_{1}

y_{1}

) közös pont. Ugyanezek állnak

T_{2}

-re,

x_{2}

-re. Ha viszont a közös pontban

x_{1} = 0

, ti. a fenti

T

pontban, akkor

m = \sqrt[]{2} > 1

, tehát az

y

tengely a valós tengely,

T

a hiperbola csúcsa, a kör és a hiperbola érintkezése nyilvánvaló.

Mindezek szerint

m

lehetséges értékei:

| m | \leq \sqrt[]{2}

| m | \neq 1

. A koordináta‐rendszertől függetlenítve, a vizsgált állítás azokra az

e

egyenesekre érvényes, amelyek a négyzet

O

középpontját tartalmazó

H_{1} E H_{2}

szögtartományban haladnak, ahol

H_{1}

H_{2}

O

pont tükörképe

A D

-re, ill.

B C

-re, kivéve az

A C

B D

átlókkal párhuzamos egyeneseket.

Szendrei Ágnes (Szeged, Ságvári E. Gyak. Gimn.)

Selényi Péter (Budapest, Kvassay J. Hídép. Techn.)

Megjegyzések. 1. A közös pontbeli érintők azonosságát igazolhatjuk azzal is, hogy a kör alsó és a hiperbola felső felét leíró

\begin{matrix} y = - \sqrt[]{1 - x^{2}}, y = - m \sqrt[]{2} + \sqrt[]{x^{2} + m^{2} - 1} \end{matrix}

függvények deriváltja a fent kapott

x_{1}

x_{2}

, helyeken egyenlő. Az

m = 0

esetben pedig, amikor

| x_{12} | = 1

, és e helyeken egyik függvénynek sincs deriváltja,

P

és

Q

a hiperbola csúcsai, közvetlenül látható, hogy az állítás igaz.
2. Számos dolgozat az érintkezést avval tekintette bizonyítottnak, hogy (5) diszkriminánsa 0, csak egy gyöke van. Láttuk azonban, hogy 2 közös pont van (bizonyos

m

-ekre), csupán ordinátáik egyenlők. Ebből tehát nem következik az érintkezés. Említi a tankönyv is^{$^{*}$}, hogy a közös pontok száma nem lényeges a valamely helyen való érintkezés szempontjából.
Ez az algebrai meggondolás méginkább azért nem teljes értékű, mert önmagában nem lenne alkalmas pl. az

y = sin x

és az

{(x - π / 2)}^{2} + y^{2} = 1

egyenletű görbék érintkezésének vizsgálatára.

^{$^{*}$}Ide és a továbbiakra vonatkozóan lásd: Hack Frigyes‐Kugler Sándorné: Függvénytáblázatok. Matematikai és fizikai összefüggések. Tankönyvkiadó. Budapest. 1968. 86‐87. old., 386. 1‐386. 7. számú összefüggések.

^{$^{*}$}Lásd Czapáry E.‐Horvay K.‐Pálmay L.: Matemetika a gimn. III. o. számára. Tankönyvkiadó. Budapest. 1968. 294.