Kezdőlap


Feladat:	F.1713	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Angyal J. , Bacsó G. , Bodnár I. , Bognár B. , Chikán B. , Fazekas Á. , Ferró J. , Füredi Z. , Földes T. , Gál Péter , Gáspár Gy. , Géczi Magdolna , Glódy A. , Hermann P. , Hoffer J. , Hollósy G. , Kérchy L. , Kertész Á. , Kiss Ipoly , Komornik V. , Kovács Zoltán , Kuhár J. , Molnár Mihály , Mózes L. , Péter Erika , Petz D. , Pósfai J. , Prácser E. , Pressing L. , Rozics G. , Rudas T. , Sailer K. , Schmidt F. , Simon Júlia , Szendrei Ágnes , Szendrei Mária , Szente J. , Szepesi L. , Vajnági A. , Vámos Gabriella , Varsányi I. , Zulauf Erzsébet
Füzet:	1971/január, 11 - 13. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Szélsőérték differenciálszámítással, Csonkakúp, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1970/április: F.1713

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kúp tengelymetszete trapéz, mely a félgömbből kimetszett félkörbe van beleírva, a trapéz hosszabbik párhuzamos oldala a félkör átmérője. Ezt választjuk hosszegységnek és a csonka kúp $a$ oldalvonalát és kisebbik alapjának $d$ átmérőjét ‐ a trapéz szárát és rövidebb párhuzamos oldalát ‐ kifejezzük az átló és a párhuzamos oldalak közti 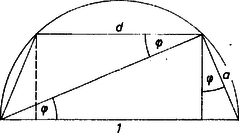$φ$ szöggel:

\begin{matrix} a = sin φ = t, d = 1 - 2 sin^{2} φ = 1 - 2 t^{2}, ahol t = sin φ . \end{matrix}

Ezekkel a csonka kúp felszínének változó része (az alsó alapkör állandó területét mindjárt elhagyva)

\begin{matrix} F = {(\frac{d}{2})}^{2} π + \frac{π + d π}{2} \cdot a, \end{matrix}

és célszerű lesz a következő függvényt vizsgálnunk:

\begin{matrix} y = \frac{F}{π} - \frac{1}{4} = {(\frac{1}{2} - t^{2})}^{2} - {(\frac{1}{2})}^{2} + (1 - t^{2}) t = t^{4} - t^{3} - t^{2} + t, \end{matrix}

ahol

\begin{matrix} 0 < t \leq \frac{1}{\sqrt[]{2}} (< 0, 7072), hiszen 0 < φ < 45^{\circ} . \end{matrix}

(1)

Ennek ugyanis ugyanazon

t

-nél vannak a szélső értékei (az értelmezési tartományban) mint

F

-nek és ugyanolyan jellegűek.
Képezzük a deriváltat és keressük az értelmezési tartományba eső zérushelyeit:

\begin{matrix} y' = 4 t^{3} - 3 t^{2} - 2 t + 1. \end{matrix}

Egyik zérushelye

t = 1

(nem esik (1)-be), hiszen az együtthatók összege 0. A megfelelő

t - 1

gyöktényezőit kiemelve

\begin{matrix} (4 t^{3} - 4 t^{2}) + (t^{2} - t) - (t - 1) = (t - 1) (4 t^{2} + t - 1), \end{matrix}

(2)

a további két zérushelyet tehát a

4 t^{2} + t - 1 = 0

egyenlet gyökei adják. Ezek valósak és szorzatuk

- 1 / 4

, eszerint egyikük negatív, tehát az is kívül esik (1)-en. A pozitív gyök viszont benne van (1)-ben:

\begin{matrix} t_{0} = \frac{1}{8} (- 1 + \sqrt[]{17}) = 0, 3904, φ_{0} = 22^{\circ} 58, 7', \end{matrix}

csak itt lehet szélső értéke

y

-nak (és

F

-nek).
Megmutatjuk, hogy

t_{0}

-ban maximum van, ehhez

y'

-nek (2) alatti második alakját használjuk föl. Az első tényező (1)-nek minden helyén negatív, a második pedig

0 < t < t_{0}

esetén (a másodfokú egyenlet két gyöke között) negatív, hiszen a másodfokú tag együtthatója pozitív, a

t_{0} < t \leq 1 / \sqrt[]{2}

értékekre pedig pozitív. Így az előbbi rész-intervallumban

y' > 0

, a függvény nő, az utóbbiban

y' < 0

, a függvény fogy, és ez állításunkat bizonyítja.
A talált maximum-helyen a csonka kúp alkotója és fedőkörének átmérője

\begin{matrix} a = t_{0} = \frac{\sqrt[]{17} - 1}{8} = 0, 390, d = 1 - 2 t_{0}^{2} = \frac{7 + \sqrt[]{17}}{16} = 0, 696, \end{matrix}

a teljes felszín pedig (a félgömb főkörét is beszámítva)

\begin{matrix} \frac{π}{512} \cdot (149 + 51 \sqrt[]{17}) = π \cdot 0, 702 = 2, 20 területegység . \end{matrix}

Gál Péter (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)