Kezdőlap


Feladat:	F.1712	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hadik Róbert , Katona Endre
Füzet:	1971/április, 147 - 149. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Magasságpont, Trapézok, Síkgeometriai számítások trigonometria nélkül háromszögekben, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1970/március: F.1712

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Minthogy a leírt (első) szerkesztéssel egy, magán az $A B$ egyenesen fekvő pontot jelölünk ki, azért lényegtelen, hogy a trapézt az $A B$ oldal fölé kifelé vagy befelé szerkesztjük.
Látni fogjuk, hogy $C^{*}$ azonos az $A B C$ háromszög $C$ -ből induló magasságának $C_{1}$ talppontjával, és a betűzés kellő megváltoztatásával hasonló állítás adódik $A^{*}$ -ra és $B^{*}$ -ra. Ebből következik, hogy a $C^{*}$ , $A^{*}$ , $B^{*}$ pontokban felállított merőlegesek a háromszög magasságvonalai, tehát az állítás igaz, és élesebben ezt mondhatjuk: a merőlegesek a háromszög magasságpontjában metszik egymást. A mondott azonossághoz elég azt megmutatni, hogy $C_{1}$ egyenlő távolságra van $A''$ -től és $B'$ től: Valóban, az $A'' C_{1} A$ , $C A C_{1}$ , $C B C_{1}$ és $B' C_{1} B$ derékszögű háromszögek, valamint a föltevések alapján

\begin{matrix} A'' C_{1}^{2} = A'' A^{2} + A C_{1}^{2} = B C^{2} + (- C C_{1}^{2} + A C^{2}) = \\ = (B C^{2} - C C_{1}^{2}) + B' B^{2} = B C_{1}^{2} + B B'^{2} = B' C_{1}^{2}, \end{matrix}

tehát, mivel puszta távolságokról van szó,

A'' C_{1} = B' C_{1}

.
Meggondolásunk akkor is érvényes, ha

C_{1}

azonosnak adódik

A

-val vagy

B

-vel. Ezzel az előrebocsátottak szerint az állítást bebizonyítottuk.

Hadik Róbert (Makó, József A. Gimn., IV. o. t.)

II. megoldás. Térbeli meggondolással a feladat állításánál többet bizonyítunk be.
Szerkesszük a három trapézt az

A B C

háromszög oldalai fölé kifelé, ekkor az előírásokból adódó

A A' = A A''

B B' = B B''

C C' = C C''

egyenlőségre tekintettel a trapézok és a háromszög együttes alakzata felfogható, mint egy (ferdén) elmetszett (egyenes) hasáb egyik része papírmodelljének kiterített hálózata, a metszetidom nélkül. Ugyanis az

A B B' A''

trapézt

A B

mint tengely körül és az

A C C'' A'

trapézt

A C

körül forgatva az

A A''

egyenes abban a síkban mozog, amely merőleges

A B

-re és átmegy

A

-n, az

A A'

pedig abban, amely merőleges

A C

-re és átmegy

A

-n. E két sík egyetlen közös egyenese az

A

-ban a háromszög

S

síkjára állított merőleges (mert

A

-n át ez az egyetlen olyan egyenes, amely

A B

-re is,

A C

-re is merőleges), és ha

A A'

-t is,

A A''

-t is ebben az egyenesben megállítjuk, az

A A' = A A''

egyenlőség alapján

A'

és

A''

egy

A_{1}

pontban találkozik, tehát

A A_{1} ⊥ S

. Ugyanígy

B'

és

B''

egy

B_{1}

pontban,

C'

és

C''

egy

C_{1}

pontban találkozik, és

A A_{1} ∥ B B_{1} ∥ C C_{1}

, ezek a mondott hasáb oldalélegyenesei és a mondott metsző sík az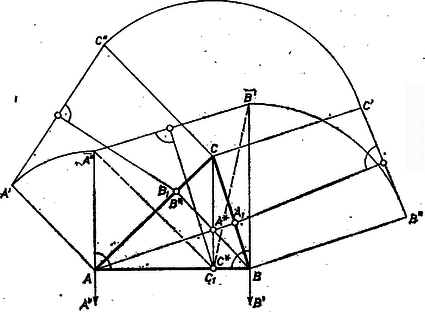

A_{1} B_{1} C_{1}

sík.

1. ábra

Azt állítjuk, hogy az

S

síkban, a

C^{*}

pontban az

A B

egyenesre állított

c^{*}

merőleges egyenes azonos az

A_{1} B_{1}

szakasz

S_{c}

felező merőleges síkjának

S

-sel való metszésvonalával. Ehhez belátjuk, hogy

c^{*}

merőleges

A_{1} B_{1}

-re.

2. ábra

S_{c}

merőlegesen áll minden olyan síkra, amely tartalmazza az

A_{1} B_{1}

egyenest, köztük az

A_{1} A B

síkra. Az utóbbira merőleges maga

S

is, tehát

S_{c}

-nek és

S

-nek

c^{* *}

metszésvonala is. Így

c^{* *}

merőleges

A B

-re, benne van

S

-ben és nyilvánvalóan átmegy

C^{*}

-on, tehát azonos

c^{*}

-gal, amint állítottuk.
Ugyanígy az (

S

síkban)

A^{*}

-ban

B C

-re merőlegesen állított

a^{*}

egyenes a

B_{1} C_{1}

szakasz felező merőleges síkjának, a

B^{*}

-ban

C A

-ra merőlegesen állított

b^{*}

egyenes a

C_{1} A_{1}

szakasz felező merőleges síkjának

S

-sel való metszésvonala.
Megmutatjuk, hogy a három felező merőleges sík egy egyenesben metszi egymást. Ugyanis

A_{1} B_{1}

és

B_{1} C_{1}

felező merőleges síkjának minden pontja egyenlő távolságra van

A_{1}

-től és

B_{1}

-től, ill.

B_{1}

-től és

C_{1}

-től, ezért e két sík

t

metszésvonalának minden pontja egyenlő távolságra van

A_{1}

-től,

B_{1}

-től és

C_{1}

-től, tehát

t

benne fekszik az

A_{1} C_{1}

szakasz felező merőleges síkjában is.
Így pedig

t

és

S

közös

L

pontja rajta van

c^{*}

a^{*}

és

b^{*}

mindegyikén; ezzel az állítást bebizonyítottuk. Nem használtuk fel az

A A_{1}

B B_{1}

C C_{1}

oldalélszakaszok hosszát, ezért az

A A' = A A'' = A A_{1}

stb. egyenlőségi föltételek teljesülése esetén a kérdéses három merőleges egyenes mindig egy pontban metszi egymást, és ez az a pont, amely egyenlő távolságra van

A_{1}

B_{1}

C_{1}

mindegyikétől.

Katona Endre (Szeged, Radnóti M. Gimn., III. o. t.)