Kezdőlap


Feladat:	F.1710	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh Zoltán , Fazekas Gábor , Füredi Zoltán , Tóth Károly
Füzet:	1970/november, 128 - 130. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletrendszerek, Paraméteres egyenletrendszerek, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1970/március: F.1710

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Összefüggésen leggyakrabban egyenlőségi kapcsolatot értünk, először ilyet írunk fel az (1)-ből kivehető két független egyenlet alapján, $t$ kiküszöbölésével. Természetesen feltesszük, hogy a nevezők egyike sem $0$ , azaz $t$ sem $π / 2$ -nek, sem $π / 3$ -nak nem egész számú többszöröse. Látjuk másrészt, hogy $x = y = z = 0$ bármely (megengedett) $t$ mellett kielégíti (1)-et, nem lehet azonban $x$ , $y$ és $z$ között vegyesen $0$ is és tőle különböző érték is. Tovább ezt is kizárjuk.
(1) első két hányadosának egyenlőségéből

\begin{matrix} \frac{y}{x} = \frac{sin 2 t}{sin t} = 2 cos t, \end{matrix}

(2)

az első és utolsóból pedig

\begin{matrix} \frac{z}{x} = \frac{sin 3 t}{sin t} = \frac{3 sin t - 4 sin^{3} t}{sin t} = 3 - 4 sin^{2} t = - 1 + 4 cos^{2} t . \end{matrix}

(3)

Ide (2)-t behelyettesítve, majd rendezéssel:

\begin{matrix} \frac{z}{x} = - 1 + {(\frac{y}{x})}^{2}, x^{2} - y^{2} + x z = 0 \end{matrix}

(4)

a kívánt jellegű, mindhárom változót tartalmazó összefüggés.
2. Kaphatunk egyenlőtlenséget is

x

és

y

, valamint

x

és

z

között (2), ill. (3) alapján:

\begin{matrix} | cos t | < 1 miatt | \frac{y}{x} | < 2, | y | < 2 \cdot | x |, \end{matrix}

(5)

egyenlőség nem állhat fenn

sin t \neq 0

miatt. Továbbá

\begin{matrix} - 1 \leq \frac{z}{x} < 3, \end{matrix}

(6)

amit így is mondhatunk: ha

z

és

x

egyenlő előjelűek, akkor

| z | < 3 \cdot | x |

ha pedig ellentett előjelűek, akkor

| z | \leq | x |

.
3. Megjegyezzük még, hogy megfordítva, (4) teljesüléséből nem következik (1), de már minden a (4)-et, (5)-öt, (6)-ot és az

x y z \neq 0

feltételt is teljesítő

x

y

z

számhármashoz van egy és csak egy olyan

t

a nyitott (

0

π / 3

), (

π / 3

π / 2

), (

π / 2

2 π / 3

) és (

2 π / 3

π

) intervallumok valamelyikében, amellyel teljesül (1)

Füredi Zoltán (Budapest, Móricz Zs. Gimn., II. o. t.)

Megjegyzés. Érdemes megnézni, mi van a kérdés mögött. Ha egy

x

y

z

számhármashoz van olyan

t

, hogy teljesül (1) és

x y z \neq 0

, akkor

k x

k y

k z

-hez ugyanaz a

t

tartozik hozzá. Ha tehát az

x

y

z

számhármast egy

P

pont térbeli derékszögű koordinátáinak tekintjük, akkor a

P

-t az

O

origóval összekötő egyenes minden pontja megfelelő (természetesen

k < 0

is lehet).
Jelöljük az (1) hányadosok közös értékét

d

-vel, tekintsük az

\begin{matrix} x = d sin t, y = d sin 2 t, z = d sin 3 t \end{matrix}

számokat egy téglatest éleinek és helyezzük el ezt úgy, hogy egy-egy

x

y

z

hosszúságú éle rendre az

x

y

, ill.

z

-tengelyre essék. Ekkor a test

O

-ból induló testátlója éppen az előbb mondott egyenesen van rajta.

t > 60^{\circ}

esetén a negatívnak adódó él (vagy élek) abszolút értékét vesszük és a téglatestet úgy illesztjük be, hogy ez az él az illető tengely negatív felére essék.

t

változásával a testátló egyenese várhatóan egy kúpszerű felületet ír le, melynek csúcsa az origó. Ezt a sejtést vázoljuk.
Az origót körülvesszük az

x = \pm 1

y = \pm \sqrt[]{2}

z = \pm 1

síkokkal körülzárt négyzetes hasábbal, és megkeressük a (4) egyenletű felület közös pontjait a határoló

4

téglalappal és

2

négyzettel (1. ábra, az elülső sík: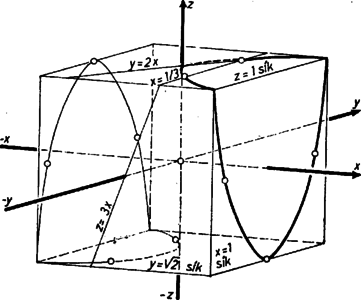

y = - \sqrt[]{2}

1. ábra

x = 1

síkon az adódó

z = y^{2} - 1

parabola

| y | \leq \sqrt[]{2}

ívének pontjait kapjuk az (

y = 0

z = - 1

) és az (

y = \pm 1

z = 0

) pontok nélkül, ezek ugyanis

t = 90^{\circ}

-nak,

60^{\circ}

-nak,

120^{\circ}

-nak felelnének meg. (Az

x = - 1

síkon az előbbi ív tükörképét kapjuk az origóra, hasonlóan

y = - \sqrt[]{2}

z = - 1

esetét sem kell külön vizsgálni.)

y = \sqrt[]{2}

esetén csak az (

x = 1

z = 1

) és a (

- 1

- 1

) pont teljesíti az adódó

x^{2} + x z = x (x + z) = 2

egyenletet (hiszen

| x | \leq 1

| z | \leq 1

, és így

| x + z | \leq 2

z = 1

esetén pedig az

x = y^{2} - x^{2}

, másképpen

\begin{matrix} \frac{{(x + 0, 5)}^{2}}{0, 25} - \frac{y^{2}}{0, 25} = 1 \end{matrix}

hiperbola két íve, az

y = 2 x

egyenessel ‐ lásd (5) ‐ való (

x = 1 / 3

y = 2 / 3

) metszésponttól (

1

\sqrt[]{2}

)-ig terjedő ív a kezdőpontja nélkül, és ennek tükörképe az

y = 0

síkra. (Megadja a kizárást (6) is.)
Más nézetben ábrázolja a kúp egy részét a 2. ábra.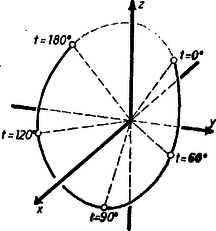

2. ábra

Mindezek szerint a kúp egyenletének a (4) alakról a paraméteres (1) alakra való átírása kizárt három elszigetelt alkotót, továbbá más két alkotó közti részét a felületnek.