Kezdőlap


Feladat:	F.1707	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Angyal J. , Bálint L. , Barbarits A. , Bartholy Judit , Boros E. , Cseresnyés Mária , Fazekas Á. , Földes T. , Gál P. , Garay B. , Gáspár Gy. , Glódy A. , Kacsuk P. , Katona Endre , Kérchy L. , Kiss Ipoly , Komornik V. , Kuhár J. , Máté Gy. , Pataki B. , Pataki L. , Prőhle T. , Schmidt F. , Simon Júlia , Szabados Gy. , Szász Gy. , Szendrei Ágnes , Szendrei Mária , Vajnági A.
Füzet:	1971/január, 7 - 9. oldal		PDF \| MathML
Témakör(ök):	Gráfelmélet, Sakk, Sakktáblával kapcsolatos feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1970/március: F.1707

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A P. 26. problémában^{$^{*}$} bizonyítva láttuk, hogy a $4 \times k$ méretű sakktábla ( $k = 3$ és $k \geq 5$ ) egymás utáni lóugrásokkal, minden mezőre egyszer lépve csak úgy járható be, ha először az egyik olyan résztartományát járjuk be, amely a szélső sorok ( $1 \times k$ méretű téglalapok) valamelyik színű mezőiből és a középső sorok ellentétes színű mezőiből áll. A bizonyítás felhasználta, hogy az összes mezőket egyszer bejárva lóugrással, csak egy olyan lépés van, amelyik belső sorból belső sorba vezet, ezzel lép át a ló az egyik résztartományból a másikba.
Ezekre támaszkodva a bejárásokat csoportosítjuk résztartományváltó lépésük szerint, külön-külön megállapítjuk az egyes csoportokba tartozó bejárások számát, végül e számokat összegezzük. Ehhez

1. megállapítjuk a résztartományváltó

E M

lépéseket, ahol

E

az első résztartomány utoljára bejárt mezejét,

M

pedig a második résztartomány elsőnek bejárt mezejét jelöli.

2. minden egyes

E

-hez és

M

-hez mint kiindulóponthoz megállapítjuk saját résztartománya bejárási lehetőségeinek számát (vagyis most az első résztartományt visszafelé járjuk be), legyen ez egy bizonyos

E M

pár esetében

e

, ill.

m

3. minden egyes, az

E

-hez vezető mondott bejárást visszafordítva összekapcsolunk minden egyes, az

M

-ből induló, mondott bejárással egy-egy teljes bejárásává a táblának, eszerint a mondott

E M

-hez

e m

számú teljes bejárás tartozik.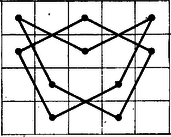

\begin{matrix} \begin{matrix} 1 & 2 & 3 \\ 4 & 17 & 5 & 18 & 6 \\ 14 & 7 & 15 & 8 & 16 \\ 9 & 10 \\ 1.ábra \end{matrix} \begin{matrix} A & B & C \\ A_{1} & B_{2} & C_{1} & B_{2} & A_{1} \\ A_{2} & B_{1} & C_{2} & B_{1} & A_{2} \\ A & B & C \\ 2.ábra \end{matrix} \end{matrix}

3. ábra

Eljárásunkat megkönnyítik a tábla szimmetriái, valamint az, hogy a két résztartomány egymás tükörképe a tábla középső sorait elválasztó egyenesre. A szükséges mezőket az 1. ábra szerint számokkal jelöljük, 1‐10 az elsőnek bejárandó résztartomány mezői, közülük 4‐8 az

E

mezők, 14‐18 pedig a második tartomány

M

mezői. Az így megállapítandó

e m

összegnek a kétszerese lesz a keresett szám, hiszen nyilvánvalóan minden útvonal oda-vissza bejárható.

A 2. ábrán a középső sorok mezőit oszlopuk helyzete és a tábla függőleges szimmetriatengelyére tükrös voltuk alapján

A

B

C

betűkkel és a tartományt jelző indexszel is megjelöltük; nyilvánvalóan mindegyik

A_{i}

(

i = 1, 2

) típusú mezőből indulva a maga résztartománya ugyanannyiféleképpen járható be, és ugyanez áll a

B_{i}

, valamint a

C_{i}

mezőkre; legyenek e számok (a fönti

e

és

m

konkrét értékei)

a

b

és

c

.
A tartományváltó lapos ugrások száma 6, közülük 2‐2

A_{1} C_{2}

C_{1} A_{2}

, ill.

B_{1} B_{2}

típusú (pl. 4‐15 és 6‐15 az első típusúak), eszerint a tábla összes bejárásainak száma

N = 2 (2 a c + 2 c a + 2 b^{2}) = 8 a c + 4 b^{2}

Megjegyezzük még, hogy a szélső (

A

-) oszlopok; mezőiről 2‐2 mezejére léphet a ló az illető tartománynak, a

B

mezőkről 3-ra, a

C

mezőkről pedig 4-re. Ez a szélső oszlopok mezőin való áthaladás 2‐2 lépését egyértelműen összekapcsolja:

\begin{matrix} - 5 - 1 - 7 -, - 2 - 4 - 9 -, - 5 - 3 - 8 -, - 2 - 6 - 10 -, \end{matrix}

kivéve ha az illető mező kezdő- vagy végpontja a tartomány bejárásának (tehát a négy egymás utáni hármasból legalább kettő minden bejárásban megtalálható valamelyik irányban). Ilyen blokká kapcsolódhat négy egymás utáni lépés is:

\begin{matrix} - 7 - 1 - 5 - 3 - 8 -, ill. - 9 - 4 - 2 - 6 - 10 -, \end{matrix}

ti. ha 1 és 3, ill. ha 4 és 6 egyike sem végpont.

Mármost az

A

B

C

típusú

E

- (ill.

M

-) mezők konkrét mintapéldájának rendre a 4-es, 7-es, 5-ös mezőt véve, az első tartomány bejárásai ‐ rendszeres próbálgatás eredményeként ‐ az alábbiak; 2‐2 szomszédos, közös kezdőszakasszal bíró bejárás zárójelbe foglalt részei egymásnak megfordításai.

\begin{matrix} \begin{matrix} (I) & 4 - 9 - 5 - (1 - 7 - 10 - 6 - 2 - 8 - 3) \\ (II) & - (3 - 8 - 2 - 6 - 10 - 7 - 1) \\ (III) & 4 - 9 - 8 - (2 - 6 - 10 - 7 - 1 - 5 - 3) \\ (IV) & - (3 - 5 - 1 - 7 - 10 - 6 - 2) \\ (V) & 4 - 9 - 8 - 3 - 5 - (1 - 7 - 2 - 6 - 10) \\ (VI) & - (10 - 6 - 2 - 7 - 1) \\ (VII) & 4 - 2 - 6 - 10 - 7 - 1 - 5 - (3 - 8 - 9) \\ (VIII) & - (9 - 8 - 3) \end{matrix}} a = 8 \\ \begin{matrix} (IX) & 7 - 1 - 5 - (3 - 8 - 9 - 4 - 2 - 6 - 10) \\ (X) & - (10 - 6 - 2 - 4 - 9 - 8 - 3) \\ (XI) & 7 - 10 - 6 - 2 - 4 - 9 - 8 - 3 - 5 - 1 \end{matrix}} b = 3 \\ \begin{matrix} (XII) & 5 - (1 - 7 - 10 - 6 - 2 - 4 - 9 - 8 - 3) \\ (XIII) & - (3 - 8 - 9 - 4 - 2 - 6 - 10 - 7 - 1) \end{matrix}} c = 2 \end{matrix}

Ezek szerint

a = 8

b = 3

és

c = 2

, tehát a táblának

N = 164

bejárása van.

Katona Endre (Szeged, Radnóti M. Gimn., III. o. t.)

Megjegyzések. 1. Az (I)‐(XIII) bejárásokat a következő észrevétel páronként egymásra, ill. önmagukra képezi le (és így bizonyos szempontból a teljesség ellenőrzésének is tekinthető). Bármely bejárás alapján felírható egy újabb, az első tartomány minden mezeje helyére a vele egy oszlopban állót írva, azaz a bejárásban az

1 - 4

7 - 9

2 - 5

8 - 10

3 - 6

mezőpárokat fölcserélve (igazolását az olvasóra hagyjuk). Pl. (III)-ból:

\begin{matrix} 1 - 7 - 10 - 5 - 3 - 8 - 9 - 4 - 2 - 6, \end{matrix}

(III

'

)

ennek a függőleges tengelyekre való tükörképe (vagyis

1 - 3

4 - 6

...

fölcserélése, 2 és 5 helyükön hagyása):

\begin{matrix} 3 - 8 - 9 - 5 - 1 - 7 - 10 - 6 - 2 - 4, \end{matrix}

(III

''

)

fordított sorrendben a (VIII)-at adja. ‐ (XII) és (XIII) egymás tükörképei, mindkettőhöz a (IV) tartozik így hozzá.

2. A (IV), (IX), (XI)‐(XIII) bejárások kezdő- és végpontja lóugrásnyira van egymástól, vagyis a féltábla bejárása záródik; mind az ötöt a 3. ábra szemlélteti, más-más lépés kiiktatásával.^{$^{*}$}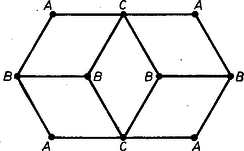

4. ábra

3. Feladatunk ekvivalens a 4. ábra gráfja szögpontjainak nyílt bejárásával, valamelyik szögpontból indulva és a gráf élei mentén haladva minden csúcsain át kell haladni egyszer.

Katona Endre

^{$^{*}$}Lásd K. M. L. 39 (1969) 151. o.

^{$^{*}$}Lásd: Tusnády Gábor ‐ Surányi János ‐ Bakos Tibor: A $4 \times k$ méretű sakktábla bejárása, K. M. L. 40 (1970) 2‐4. o.