Kezdőlap


Feladat:	F.1706	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barbarits András
Füzet:	1971/február, 57 - 58. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Egyenlő szárú háromszögek geometriája, Térelemek és részeik, Tetraéderek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1970/február: F.1706

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Közös oldaluk és az adott élegyenlőségek alapján az $A B D$ és $D C A$ háromszöglapok egybevágók ‐ csúcsaik páronként a mondott felsorolás rendjében felelnek meg egymásnak ‐ és egyező körüljárásúak (természetesen mindkét lapot kívülről szemlélve). Ezért, $A D$ felezőpontját $E$ -vel jelölve $E B = E C$ , a $B C E$ háromszög egyenlő szárú, és a $B C$ él felezőpontját $F$ -fel jelölve 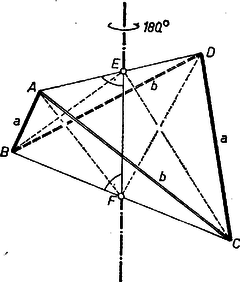$E F ⊥ B C$ .

Ugyanígy adódik

B A C Δ ≅ C D B Δ

F A = F D

és

F E ⊥ A D

. Eszerint a tetraédert

E F

mint tengely körül

180^{\circ}

-kal elfordítva az

A

D

, valamint

B

C

csúcspárok egymásba mennek át, az egész tetraéder önmagába, a föltevés szerint egyenlő hosszú élek is egymásba. Ebből következik az egyenlő élpároknál levő lapszög-párok egyenlősége.
2. Legyen a

D

csúcs merőleges vetülete az

A B C

lapon, az

A B

és az

A C

egyenesen rendre

D_{0}

D_{b}

D_{c}

így a kérdéses lapszögek sinusa, és arányuk

\begin{matrix} sin C (A B) D = \frac{D D_{0}}{D D_{b}}, sin B (A C) D = \frac{D D_{0}}{D D_{c}} \\ \frac{sin C (A B) D}{sin B (A C) D} = \frac{D D_{c}}{D D_{b}}, \end{matrix}

vagyis az

A C D

háromszögben az

A C

, ill. az

A B D

háromszögben az

A B

alaphoz tartozó magasságok aránya. Minthogy pedig a két háromszög ‐ mint láttuk ‐ egybevágó, tehát egyenlő területű, azért a mondott magasságok fordítva arányosak a megfelelő alapokkal:

\begin{matrix} \frac{D D_{c}}{D D_{b}} = (\frac{1}{A C}) : (\frac{1}{A B}) = \frac{a}{b} . \end{matrix}

Ezt kellett bizonyítanunk.

Barbarits András (Budapest, I. István Gimn., IV. o. t. )