Kezdőlap


Feladat:	F.1704	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Angyal J. , Balogh Z. , Füvessy L. , Gál P. , Garay B. , Kacsuk P. , Kiss Ipoly , Komornik V. , Kuhár J. , Máté Gy. , Papp Gábor , Pintér Vera , Selényi P. , Simon Júlia , Szabados Gy. , Szász Gy. , Szendrei Ágnes , Szendrei Mária
Füzet:	1970/november, 126 - 128. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Magasságvonal, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1970/február: F.1704

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen a kérdéses $A B C$ háromszög $A B$ átfogója egységnyi, kisebbik hegyesszöge $B A C ∢ = α$ , így befogói $A C = cos α$ és $B C = sin α$ , rövidítsük ezeket rendre $c$ , $s$ betűvel. A követelmény szerint $c^{2} = 1 \cdot s$ , így Pitagorasz tétele alapján

\begin{matrix} s^{2} + s - 1 = 0, s = \frac{\sqrt[]{5} - 1}{2} (\approx 0, 6180) . \end{matrix}

Eszerint a háromszög megkapható az egységnyi sugarú körbe írt szabályos tíz- (és öt-)szög oldala ismert (ún. Ptolemaiosz ‐ Dürer-féle) szerkesztésének egy lépéssel való kiegészítése útján, a

k

kör középpontja

B

, a tízszögoldal

B C

és a

C

-ben emelt merőlegesnek

k

-n levő pontja

A

(1. ábr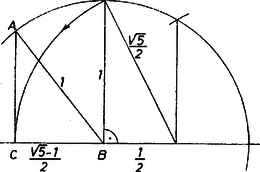a).

1. ábra

II. Jelöljük a derékszög csúcsából húzott magasság talppontját az egymás utáni háromszögekben az alábbiak szerint (2. ábra):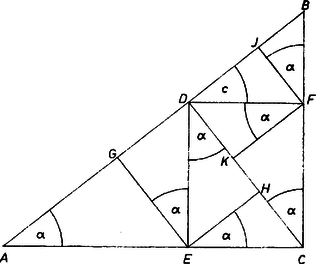

2. ábra

háromszög:

A B C, A C D, B C D, A D E, C D E, B D F, C D F

,
talppont:

D, E, F, G, H, J, K

.

A keletkezett háromszögek hasonlók, mindegyik befogó egy továbbosztással keletkezett háromszögben átfogó lesz, így a szakaszok legtöbbje mint vetület fejezhető ki

s

-sel és

c

-vel, ill. a követelmény szerint egyedül

c

-vel:

\begin{matrix} \begin{matrix} D C = A C sin α = B C cos α = c s = c^{3}, \\ D A = A C cos α = c^{2}; & D B = B C sin α = s^{2} = c^{4}; \\ E D = C F = C D cos α = c^{4}, & F D = C E = C D sin α = c^{3} s = c^{5}, \\ E A = c^{3}, & F B = c^{6}; \\ G E = D H = c^{5}, & G D = E H = c^{6}, & G A = c^{4}, & H C = c^{7}, \\ J F = D K = c^{7}, & J D = F K = c^{6}, & J B = c^{8}, & K C = c^{5}; \end{matrix} \end{matrix}

végül azok a megrajzolt szakaszok, amelyek nem oldalai a fenti háromszögek valamelyikének:

\begin{matrix} A J = A B - J & B = 1 - c^{8} = 1 - s^{4} = (1 - s^{2}) (1 + s^{2}) = c^{2} \cdot \sqrt[]{5} s = \sqrt[]{5} c^{4}, \\ B G = A B - A G = 1 - c^{4} = 1 - s^{2} = c^{2}, \\ G J = G D + D J = 2 c^{6}, \\ H K = C K - C H = c^{5} (1 - c^{2}) = c^{5} s^{2} = c^{9} . \end{matrix}

Ezek szerint a

10

pont közti megrajzolt

28

szakasz közül

26

-nak a mértékszáma

c

-nek valamely nem negatív egész kitevős hatványával egyenlő. Mondjuk így: e szakaszok mindegyikéhez tartozik

c

-nek egy kitevője, és fordítva: a

0, 1, ..., 9

kitevők mindegyikéhez hozzátartozik az ábrának legalább egy szakasza. A kitevők szerint csoportosítva:

\begin{matrix} c^{0} & = A B & c^{5} & = F D, C E, E G, D H, K C \\ c & = A C & c^{6} & = B F, D G, E H, J D, F K \\ c^{2} & = B C, A D, B G & c^{7} & = C H, J F, D K \\ c^{3} & = C D, A E & c^{8} & = J B \\ c^{4} & = B D, E D, C F, A G & c^{9} & = H K \end{matrix}

a hátra levő 2 szakasz pedig egy

c

-hatvány állandószorosa:

\begin{matrix} A J = \sqrt[]{5} c^{4}, G J = 2 c^{6} . \end{matrix}

(1)

Így minden olyan szakaszpárnak megtalálható a mértani középarányosa, amelynek a kitevői egyenlő párosságúak (és természetesen különbözők), pl.

A B

és

B F

mértani középarányosát adja

C D

is,

A E

is. És fordítva: a talált mértani sorozat első és utolsó tagját (

A B

-t és

H K

-t) kivéve minden szakaszhoz található olyan két (tőle különböző) szakasza az ábrának, melyeknek ő mértani középarányosa, pl.

J B

-hez egyrészt

H K

, másrészt

C H

J F

és

D K

bármelyike.
Az (1) szakaszok viszont ilyen szakaszhármasban nem szerepelhetnek, mert

\sqrt[]{5}

, ill.

2

állandó tényezőjük

c

-nek nem egész kitevős hatványa, a szorzatuk sem, és e kitevők nem is

n + 1 / 2

alakúak, ahol

n

egész szám:

\sqrt[]{5} = c^{- 3,345}

2 = c^{- 2,881}

2 \sqrt[]{5} = c^{- 6,225}

.
Meghatározzuk végül a kérdéses szakaszpárok számát. Egy

c^{5}

hosszúságú szakasz mértani középarányos minden lehetséges (

c^{4}, c^{6}

), (

c^{3}, c^{7}

), (

c^{2}, c^{8}

) és (

c, c^{9}

) pár között, ezek megválasztására

4 \cdot 5 + 2 \cdot 3 + 3 \cdot 1 + 1 \cdot 1 = 30

lehetőség van. (Ha még azt is nézzük, hogy a

c^{5}

hosszú mértani közép szerepére az

5

ilyen szakasz melyikét választjuk, akkor az ilyen szakaszhármasok száma

5 \cdot 30 = 150

.) Hasonlóan

\begin{matrix} c, c^{2}, c^{3}, c^{4}, c^{6}, c^{7}, c^{8} \end{matrix}

hosszúságú mértani közepet ad rendre

\begin{matrix} 3, 6, 22, 29, 21, 10, 3 \end{matrix}

(különböző hosszúságú) szakaszpár, tehát a párok összes száma 124. (Az egyenlő hosszú szakaszok közti ilyen kapcsolatokat figyelmen kívül hagytuk.)

Szendrei Ágnes (Szeged, Ságvári E. Gyak. Gimn., III. o. t.)