| Feladat: | F.1703 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1970/november, 125 - 126. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Határozott integrál, Parabola egyenlete, Terület, felszín, Parabola, mint kúpszelet, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1970/február: F.1703 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Minden parabola hasonló (egyetlen lineáris adat határozza meg, a fókusznak a vezéregyenestől való távolsága), ezért elég az állítást az egyenletű parabolára igazolni. Ennek vezéregyenese párhuzamos az tengellyel, azt kell tehát belátnunk, hogy ha egy változó helyzetű húr , végpontjainak abszcisszái és , vagyis a kérdéses vetület hossza , ahol pozitív állandó, pedig tetszés szerinti érték, akkor a húr által lemetszett parabolaszelet területe nem függ -től. 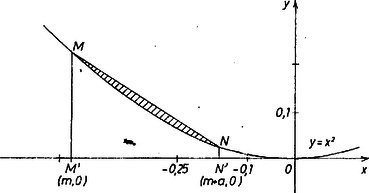 A trapéz területe, mivel párhuzamos oldalai az és ordináták, magassága (szélessége) , Megjegyzés. Természetesen a húr alatti trapéz területét is számíthattuk volna integrállal. A húr a |