Kezdőlap


Feladat:	F.1702	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balog J. , Balogh Z. , Barbarits A. , Chikán B. , Czédli G. , Fazekas Á. , Ferró J. , Frankl P. , Füredi Z. , Földes T. , Gáspár Gy. , Glódy A. , Görbe M. , Hermann P. , Hermann T. , Horváthy P. , Katona E. , Kelen M. , Kérchy L. , Kiss Ipoly , Lakatos B. , Lévai G. , Martoni V. , Máté Gy. , Nagy István (II. o., Veszprém) , Nyilánszky M. , Papp Gábor , Papp László , Pataki B. , Pekár Gy. , Petz D. , Poór Zs. , Prácser E. , Pressing L. , Selényi Péter , Szabó Lóránt , Szendrei Ágnes , Szendrei Mária , Tóth Béla , Turán Gy. , Vajnági A. , Wittmann Imre
Füzet:	1970/október, 58 - 59. oldal		PDF \| MathML
Témakör(ök):	Összefüggések binomiális együtthatókra, Számelrendezések, Feladat
Hivatkozás(ok):	Feladatok: 1970/február: F.1702

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feladatunkban a binomiális együtthatóknak csupán a páros vagy páratlan voltát kell tekintenünk, ezért megtehetjük, hogy a párosokat 0-sal, a páratlanokat 1-essel helyettesítjük. Az így módosított számelrendezésre is nyilvánvalóan érvényes a Pascal-háromszög elemeinek képezési eljárása: minden belső elem a fölötte álló két elem összege ‐ de két szomszédos 1-es alatt középen 2 helyett 0 áll ‐, továbbá minden sor két szélső eleme 1-es. Az új séma 1-eseinek számát kell megállapítanunk azokig az egyenesekig, amelyek a sémából $2^{n}$ számú sort vágnak le a csúcsától számítva, 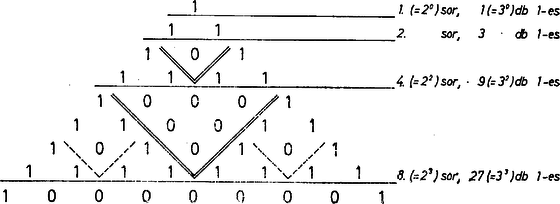$n = 0, 1, 2$ .
$...$ . Megjegyezzük, hogy az $(\binom{u}{v})$ , $0 \leq v \leq u$ együtthatók az $(u + 1)$ -edik sorát alkotják a sémának.
Felírva a módosított séma első 9 sorát, azt látjuk, hogy $n = 0, 1, 2, 3$ esetén a $2^{n}$ sorszámú sorig bezárólag az 1-esek száma valóban $3^{n}$ . A leszámlálás helyett $n = 3$ esetén elég azt észrevenni, hogy a $2^{2}$ és $2^{3}$ számú sort levágó vízszintes vonalak közti trapézt a berajzolt ferde vonalakkal 3 háromszögre vágva a két szélső háromszög ,,egybevágó'' a sémának a trapéz fölötti háromszögével (azaz helyről helyre ugyanazt a számot tartalmazza), a közbülső háromszög pedig egyetlen 1-est sem tartalmaz. Így a trapézban 2-szer annyi 1-es áll, mint fölötte, tehát azokat is véve, együttes számuk 3-szor annyi, mint a felső háromszögben.

Megmutatjuk, hogy a figyelembe vett sorok számát

2^{n}

-ről

2^{n + 1}

-re emelve ‐ azaz megkétszerezve ‐ ez a tulajdonság megismétlődik. Így ‐ ha az első

2^{n}

sorban levő 1-esek száma

N

, akkor az első

2^{n + 1}

sorban levők száma

(1 + 2) N =

= 3 N

. Ehhez csupán azt tesszük föl, hogy a

2^{n}

sorszámú sor minden eleme 1-es (ahogyan

n = 0, 1, 2, 3

-ra látjuk), szám szerint

2^{n}

db 1-esből áll (hiszen a séma minden sora annyi elemet tartalmaz, amennyi a sorszáma).
Feltevésünk folytán a

(2^{n} + 1)

-edik sorba a

2^{n}

-edik sor

(2^{n} - 1)

szomszédos párja alá ugyanennyi 0 kerül belső elemként, mivel

1 + 1

páros és csupán a külön szabály szerint képezett két szélső elem lesz 1-es. A mondott 0-ok szomszédos párjai alá ismét 0 kerül, számuk 1-gyel kevesebb, hiszen

e

elemből

(e - 1)

szomszédos pár képezhető, vagyis itt

(2^{n} - 2)

. Ez ismétlődik a

2^{n} + (2^{n} - 1) = (2^{n + 1} - 1)

-edik sorig, amíg a 0-ok száma 1-re csökken, tehát kialakul a 0-ok háromszöge. Így pedig a

(2^{n} + 1)

-edik sor első és utolsó 1-eséből a trapéz két szélső háromszöge valóban ugyanúgy alakul ki, mint a séma első

2^{n}

sora (azzal valóban ,,egybevágók'') és a

2^{n + 1} = 2 \cdot 2^{n}

-edik sor

2 \cdot 2^{n}

számú 1-esből áll, a föltett tulajdonság a

2^{n}

-edik sorról öröklődik a

2^{n + 1}

-edik sorra.
Ez pedig az előrebocsátottak szerint az 1-esek számának megháromszorozódását jelenti, az állítást bebizonyítottuk.

Selényi Péter (Budapest, Kvassay J. Híd-és Vízműépítési Techn., Ill. o. t.)

Megjegyzés. Meg lehet mutatni azt is, hogy a Pascal-háromszög minden egyes sorában a páratlan együtthatók száma

2^{k}

alakú, ahol

k \geq 0

, egész.