Kezdőlap


Feladat:	F.1699	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Skopál István
Füzet:	1970/november, 123 - 125. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Síkgeometriai számítások trigonometria nélkül, Szinusztétel alkalmazása, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1970/január: F.1699

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A $K$ pont csak a háromszög belsejében lehet. Ha ugyanis $K$ a síknak $A$ -tól a $B C$ egyenes által elválasztott pontja, és az $A B C$ háromszög pozitív körüljárású, akkor $0 < K B C ∢ < π$ (forgásszög főértékének a $- π$ és $π$ közti értékét véve), viszont $K A B ∢$ és $K C A ∢$ közül legalább az egyik $- π$ és $0$ közé esik (1a és b ábra).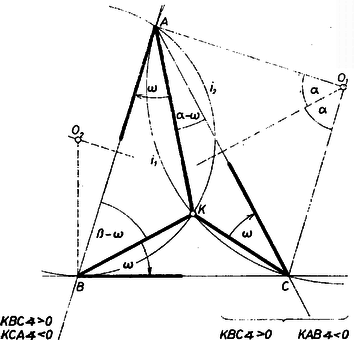

1a. ábra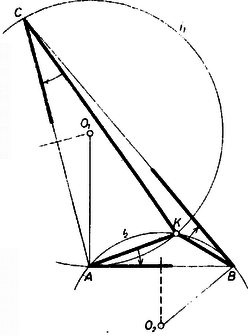

1b. ábra

Megállapításunkból élesebben az következik, hogy a három forgásszög iránya ellentétes a háromszög csúcsai

A

B

C

sorrendű körüljárásának irányával, és abszolút értéke kisebb, mint a háromszög legkisebb szöge.
Legyen egy, a háromszög belsejében levő

K

pontra a három forgásszög közös értéke

ω

, ekkor

K A C ∢ = α - ω

K B A ∢ = β - ω

, és a

C A

A B

oldalnak

K

-ból vett látószöge rendre

C K A ∢ = 180^{\circ} - α

A K B ∢ = 180^{\circ} - β

, tehát

K

megszerkeszthető a megfelelő

i_{1}

, ill.

i_{2}

látókörív közös pontjaként. Az

i_{1}

-et tartalmazó kör

O_{1}

középpontjánál levő szög

A O_{1} C ∢ = 2 α

, így

C A O_{1} ∢ = 90^{\circ} - α

(előjellel együtt értve), tehát

B A O_{1} ∢ = B A C ∢ + C A O_{1} ∢ = 90^{\circ}

, eszerint

O_{1}

A

-ban

A B

-re állított merőlegesnek és

A C

felező merőlegesének közös pontja, más szóval:

O_{1}

, a

C

-n átmenő és

A B

-t

A

-ban érintő kör középpontja. Eszerint

i_{1}

e körnek az az

A C

íve, mely az

A C

egyenesnek

B

-t tartalmazó partján van.

i_{2}

pedig hasonlóan az

A

-n átmenő és

B C

-t

B

-ben érintő körnek az az íve, amely az

A B

egyenesnek

C

-t tartalmazó partján van. Ezzel eljárást adtunk

K

megszerkesztésére.

i_{1}

és

i_{2}

A

-n kívül egy további pontban metszik egymást ‐ ez

K

‐, mert

A

-beli érintőik szöget alkotnak, nagysága

β

. Az

i_{1}

i_{2}

ívek, és így

K

is a

B A C

szögtartományban vannak, éspedig a háromszög belsejében, mert az

i_{2}

-t tartalmazó kör csupán érinti

B C

-t és áthalad

A

-n. Ezek alapján

A C K ∢ = B A K ∢

, mert az

i_{1}

-nek

A K

rész-ívén nyugvó kerületi szögek, és ugyanígy

B A K ∢ = C B K ∢

, tehát a

K

pont megfelel a követelménynek.
A végzett szerkesztés bármely háromszögben végrehajtható, minden háromszögben egyértelműen létezik a

K

pont.
II. A

K C A

és

K C B

háromszögekből a sinustétel alapján, majd az addíciótételt alkalmazva

\begin{matrix} K C = \frac{A C sin (α - ω)}{B C sin (180^{\circ} - α)} = \frac{B C sin ω}{sin (180^{\circ} - γ)}, \\ b sin γ sin α cos ω - b sin γ cos α sin ω = a sin α sin ω, \end{matrix}

amiből átrendezés után

\begin{matrix} ctg ω = \frac{a sin α + b sin γ cos α}{b sin γ sin α} = \frac{a}{b sin γ} + ctg α . \end{matrix}

Itt az első tag

\begin{matrix} \frac{b cos γ + c cos β}{b sin γ} = ctg γ + (\frac{c sin β}{b sin γ}) \cdot \frac{cos β}{sin β}, \end{matrix}

ennek második tagja

ctg β

, hiszen a zárójelben

1

áll, ennélfogva

\begin{matrix} ctg ω = ctg α + ctg β + ctg γ . \end{matrix}

(1)

Skopál István (Budapest, Kölcsey F. Gimn., IV. o. t.)

Megjegyzések. 1. Akkor is egyértelműen létrejön a

K

pont, ha egy háromszögben

B

és

C

betűzését felcseréljük. Ezzel a körüljárás iránya ellentétesre fordul, úgyszintén

ω

iránya is megfordul, abszolút értéke azonban (1) szerint változatlan. Az új,

K'

pontra nézve az eredeti betűzés szerinti

K' A C

K' C B

K' B A

forgásszögek egyenlők.

K'

csak akkor esik egybe

K

-val, ha

α - ω = ω = β - ω =

= γ - ω

, azaz

α = β = γ

esetén, szabályos háromszögben.

K

-t és

K'

-t a háromszög Brocard-féle pontjainak,

ω

-t pedig Brocard-féle szögének szokás nevezni. (2. ábra). ^{$^{*}$}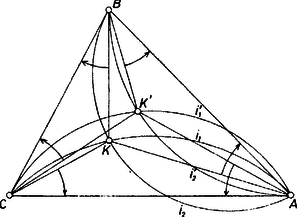

2. ábra

2. A P. 56. problémában^{$^{*}$}

ctg ω

-nak a háromszög oldalaival és területével való kifejezését használjuk fel:

\begin{matrix} ctg α = \frac{2 b c cos α}{2 b c sin α} = \frac{b^{2} + c^{2} - a^{2}}{4 t} \end{matrix}

és

ctg β

ctg γ

analóg kifejezései alapján

\begin{matrix} ctg ω = \frac{a^{2} + b^{2} + c^{2}}{4 t} \end{matrix}

Egy másik szimmetrikus kifejezés (1)-ből

sin α = a / 2 r

és az analóg kifejezések helyettesítésével, ahol

r

a háromszög köré írt kör sugara:

\begin{matrix} ctg ω = 2 r (\frac{cos α}{a} + \frac{cos β}{b} + \frac{cos γ}{c}) . \end{matrix}

^{$^{*}$} Lásd Kürtschák József‐Hajós György‐Neukomm Gyula‐Surányi János: Matematikai versenytételek, I. rész, 3. kiadás. Tankönyvkiadó, Budapest, 1965, 28‐29. o.

^{$^{*}$}Lásd ezen számban, 143. o.