| Feladat: | F.1698 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1971/február, 52 - 57. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Hiperbola egyenlete, Hiperbola, mint mértani hely, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1970/január: F.1698 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Jelöljük az adott egyenest -fel, az adott pontot -fel, az adott hegyesszöget -val, és távolságát -vel. Legyen a -en átmenő tetszőleges kör, messe -et az , pontokban, jelöljük középpontját -vel és vetülete -en legyen (1. ábra). 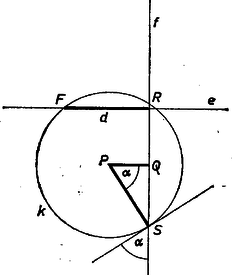 A háromszög derékszögű, és -nél levő szöge egyenlő és szögével, tehát akkor és csakis akkor tartozik a vizsgált mértani helyhez, ha ez a szög egyenlő -val. A háromszögben Ha rajta van -en, akkor azonos és egyikével, tehát rajta van a -en átmenő, -fel nagyságú szöget bezáró két egyenes egyikén (2. ábra). 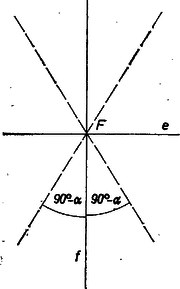 A fentiekből következik, hogy ezeknek az egyeneseknek minden, a -től különböző pontja a mértani helyhez tartozik, és ebben az esetben ez a két egyenes adja a vizsgált mértani helyet (metszéspontjukat kivéve). A továbbiakban feltesszük, hogy nincs rajta -en, azaz . Tájékozódásul megszerkesztjük a mértani helynek néhány pontját. -en át -re merőleges félegyenest rajzolunk, majd ugyancsak -en át -vel szöget bezáró félegyenest. Egy, a körül rajzolt tetszőleges kör messe -t -ban, vetülete -n legyen . Megrajzoljuk az -től távolságra levő, -fel párhuzamos , egyeneseket: ezeknek -val alkotott metszéspontjai a kívánt tulajdonságúak (3. ábra). 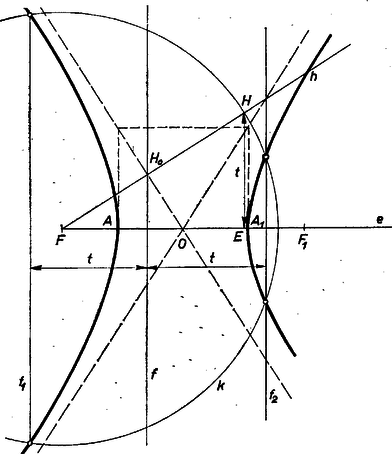 A kapott pontok alapján azt sejtjük, hogy a vizsgált mértani hely hiperbola, melynek az egyik fókusza, és a valós tengelye. Hogy ezt bizonyítani tudjuk, meghatározzuk először a sejtett hiperbolának a valós tengelyén levő pontjait és a másik fókuszát. Jelöljük ezeket -val, -gyel, -gyel és a hiperbola centrumát -val, legyen továbbá , (4. ábra). 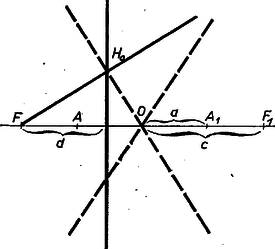 Ekkor ; ; és távolsága ; és távolsága . Mivel és a mértani helyhez tartozik: Sejtésünk igazolásához ezek szerint azt kell megmutatnunk, hogy ha egy tetszőleges pont -től mért távolsága a -től mért távolságának a -szorosa, akkor . Legyen ; ; a háromszög -nél levő szöge , ebben a háromszögben a cosinustétel alapján
ha pedig és az azonos oldalán van, akkor
amit (1)-be helyettesítve kapjuk, hogy Ezzel beláttuk, hogy a vizsgált mértani hely pontjai rajta vannak a , fókuszú, , csúcsú hiperbolán. Fordítva, ennek a hiperbolának minden pontja a mértani helyhez tartozik, hiszen ha , akkor a fenti átalakítással kapjuk, hogy (2) teljesül, amiből következik. A kapott hiperbola képzetes tengelye Megjegyzés. A mértani hely egyes pontjait a következő eljárással is kaphatjuk. Válasszuk ki -nek tetszés szerinti pontját az előírt körrel való (egyik) metszéspont céljára, ekkor az -n átmenő, -fel szöget bezáró két egyenes, , lesz egy-egy megfelelő kör -beli érintője ‐ amely az egyenes és kör metszésénél levő szög értelmezése szerint a kört a szög másik száraként képviseli. Továbbmenve a kör középpontja egyrészt az -re, ill. -re -ban állított , merőlegesen lesz, másrészt az húr felező merőlegesén (5. ábra). 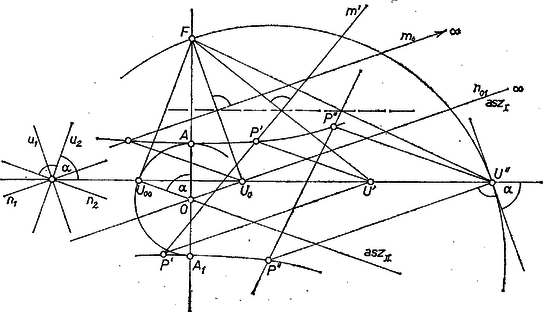 II. megoldás. Tovább használjuk az I. megoldás jelöléseit, és azt az eredményt, hogy azoknak a pontoknak a mértani helyét kell meghatároznunk, amelyeknek az egyenestől mért távolsága egyenlő a ponttól mért távolságuk -szorosával, ahol , azaz amelyekre Válasszuk meg úgy a koordináta-rendszert, hogy az tengely pozitív iránya megegyezzék a -ből induló, -re merőleges félegyenes irányával, az tengely pedig legyen. Ezek szerint koordinátái: . Egy tetszőleges pontra
tehát egyik fókusza a pont. Mivel , eredményünkből az is leolvasható, hogy az aszimptoták a valós tengellyel nagyságú szöget zárnak be, és könnyen látható az I. megoldásnak az az eredménye is, hogy a pontnak az aszimptotákra eső merőleges vetülete rajta van -en. Ha , akkor (3)-ból az egyenletet kapjuk: ez két egyenes egyenlete, melyek átmennek az origón, a tengelyre tükrözve egymásba mennek át, és iránytangensük abszolút értéke III. megoldás. Ismét az I. megoldásbeli jelöléseket használjuk és feltesszük, hogy (a esetben a 2. ábra mutatja a megoldást). Vegyünk fel tetszőlegesen egy kört, mely eleget tesz a feladat követelményeinek, és invertáljuk a pont körüli tetszőleges körre, inverzét jelöljük -vel, inverze pedig az -vel jelölt, sugarú kör legyen (6. ábra). 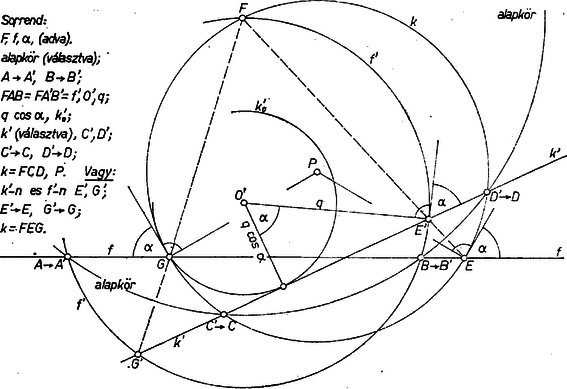 Ekkor is szög alatt metszi -t. Az ilyen tulajdonságú egyenesek azonban érintik az -vel koncentrikus, sugarú kört. Legyen inverze , akkor a kör ‐ bárhogyan is vettük fel ‐ érinteni fogja -t. Másrészt, ha egy -en áthaladó kör érinti -t, akkor inverze érinti , azaz szög alatt metszi -t, és így is szög alatt metszi -et. Keressük tehát azon körök középpontjainak mértani helyét, melyek -en átmennek, és érintik. Jelöljük középpontját -gyel, sugara legyen , akkor a mértani hely minden pontjára |