Kezdőlap


Feladat:	F.1697	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bihari Imre , Prőhle Tamás , Sashegyi László
Füzet:	1970/november, 119 - 123. oldal		PDF \| MathML
Témakör(ök):	Függvény határértéke, Két pont távolsága, szakasz hosszúsága, Síkgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1970/január: F.1697

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Ha a $P$ pont távolodik az adott $e$ egyenesen az $A$ pont $e$ -n levő $A_{0}$ vetületétől, a $B P A_{0}$ szög egyre kisebb lesz, a $B P$ egyenes egyre jobban megközelíti a $B$ -n át $e$ -vel párhuzamosan húzott $f$ egyenest (1. ábra).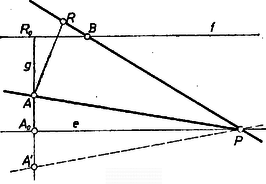

1. ábra

Az egyenlő szárú

A P R

háromszög

P

-nél levő szöge is egyre kisebb lesz, az

A R

alapon levő szögei pedig

90^{\circ}

-hoz tartanak. Az

A R

egyenes így egyre közelebb lesz az

A

-n átmenő,

e

-re merőleges

g

egyeneshez. Ezek alapján azt várjuk, hogy

R

határhelyzete az

f

és

g

egyenesek

R_{0}

metszéspontja lesz.
Sejtésünket a következő módon mondhatjuk ki pontosan: tetszőleges

ε > 0

-hoz van olyan

d

, hogy minden olyan

P

pontra, melyre

A_{0} P > d

, teljesül, hogy

R_{0} R < ε

. Ezt fogjuk bizonyítani, előbb azonban a

P R

A R

egyenesekre vonatkozó állításainkat látjuk be. Feltehetjük, hogy

A

és

B

különböző pontok, ellenkező esetben ugyanis

P

minden helyzeténél az

A

B

R

R_{0}

pontok azonosak; továbbá azt is, hogy

B

nincs rajta

e

-n.
b) Az, hogy a

B P

egyenes tart

f

-hez, esetünkben pontosabban azt jelenti, hogy tetszőleges

ω > 0

-hoz van olyan

d

, hogy ha

A_{0} P > d

, akkor a

B P

és

f

egyenesek szöge kisebb

ω

-nál, azaz a

B P

egyenes a

B

ponton átmenő,

f

-fel

ω

szöget bezáró

f_{1}

f_{2}

egyenesek közti csúcsszög-tartomány belsejében halad (természetesen

ω < 90^{\circ}

; 2. ábra).

2. ábra

f_{i}

egyenesek

e

-vel alkotott metszéspontját

F_{i}

-vel jelölve

(i = 1, 2)

, a

P B

egyenes akkor és csak akkor halad az

f_{1}

f_{2}

egyenesek által létesített szögtartományok közül az

f

-et tartalmazóknak a belsejében, ha

P

e

egyenesnek az

F_{1} F_{2}

szakaszon kívüli félegyenesein helyezkedik el. Legyen

d

A_{0} F_{1}

A_{0} F_{2}

távolságok közül a nagyobbik, ekkor az

A_{0} P > d

egyenlőtlenségből következik, hogy

P

kívül van az

F_{1} F_{2}

szakaszon, hiszen az

F_{1} F_{2}

szakasz egyik pontja sincs

A_{0}

tól

d

-nél távolabb.

d

-nek ez az értéke tehát megfelelő, ezzel a

B P

egyenesre vonatkozó állításunkat bebizonyítottuk.
c) Az

A R

egyenesre vonatkozó állításunkat hasonlóan fogalmazhatjuk meg pontosabban: tetszőleges

ω

hegyesszöghöz van olyan

d

, hogy ha

A_{0} P > d

, akkor az

A R

és

g

egyenesek közti szög kisebb

ω

-nál.
Válasszuk az

ω_{1}

ω_{2}

, hegyesszögeket egyelőre tetszőlegesen; láttuk, hogy van olyan

d_{1}

, hogy ha

A_{0} P > d_{1}

, akkor a

B P

és

f

egyenesek szöge (ami egyenlő

B P

és

e

szögével) kisebb

ω_{1}

-nél. Hasonlóan van olyan

d_{2}

, hogy ha

A_{0} P \geq d_{2}

, akkor

A P A_{0} ∢ < ω_{2}

. Ha mármost

A_{0} P

d_{1}

-nél is,

d_{2}

nél is nagyobb, akkor

A P R ∢ < ω_{1} + ω_{2}

, hiszen az

A P R

szög az

R P A_{0}

A P A_{0}

, szögeknek vagy az összegével vagy a különbségével egyenlő (aszerint, hogy

A

és

B

e

-nek két oldalán vagy ugyanazon oldalán van), így nem lehet nagyobb e szögek összegénél. Ha pedig

A P R ∢ < ω_{1} + ω_{2}

, akkor

\begin{matrix} P A R ∢ = 90^{\circ} - \frac{1}{2} A P R ∢ > 90^{\circ} - \frac{ω_{1} + ω_{2}}{2} . \end{matrix}

A R

és

g

egyenesek közti szög nem lehet nagyobb, mint annak a két szögnek az összege, amelyek közül az egyik az

A P

és

e

egyenesek szöge, a másik pedig

\frac{1}{2} A P R ∢

, amennyivel a

P A R ∢

90^{\circ}

-nál kisebb. Így az

A R

és

g

egyenesek közti szög kisebb, mint

\begin{matrix} ω_{1} + \frac{ω_{1} + ω_{2}}{2} = \frac{3 ω_{1} + ω_{2}}{2} . \end{matrix}

Ha tehát

ω_{1}

-et és

ω_{2}

-t egyenlőnek választjuk

ω / 2

-vel, akkor ez a szög kisebb

ω

-nál, hacsak

A_{0} P > d

, ahol

d = max (d_{1}, d_{2})

.
Bizonyításunk közben láttuk, hogy

d

-nek ez a választása azt is biztosítja, hogy a

B P

f

egyenesek szöge kisebb legyen

ω_{1}

-nél, tehát ez a szög is kisebb

ω

-nál.
d) Rátérünk sejtésünk bizonyítására (lásd 2. bekezdés). Legyen

ε

tetszőleges pozitív szám, és jelöljük az

R_{0} A

R_{0} B

félegyenesek közti szög felezőjét

h

-val,

Q

pedig legyen

h

-nak e szögtartományon túli részén az a pont, melyre

R_{0} Q = ε

(3. ábra).

3. ábra

(Ha

A

vagy

B

azonos

R_{0}

-lal,

h

-t az

f

és

g

egyenesek két szögfelezője közül tetszőlegesen választhatjuk.) Jelöljük az

A Q

B Q

egyeneseket

g_{1}

-gyel, illetve

f_{1}

-gyel, és legyen

f_{2}

f_{1}

-nek

f

-re,

g_{2}

pedig

g_{1}

-nek

g

-re vonatkozó tükörképe. Legyen

ω_{1}

, az

f_{1}

és

f

ω_{2}

, a

g_{1}

, és

g

egyenesek közti szög, és

ω

ω_{1}

ω_{2}

szögek közül a kisebbik, és válasszuk meg

ω

-hoz

d

-t a c) pont szerint. Eszerint ha

A_{0} P > d

, akkor a

B R

és

f

, valamint az

A R

és

g

egyenesek közti szög kisebb

ω

-nál,

B P

tehát

f_{1}

és

f_{2}

között,

A R

pedig

g_{1}

és

g_{2}

között halad. Az

A R

B P

egyenesek

R

közös pontja tehát az

f_{1}

f_{2}

és a

g_{1}

g_{2}

egyenesek által meghatározott szögtartományok belsejében van. Megmutatjuk, hogy ha

R

e szögtartományok közös részének tetszőleges pontja, akkor

R R_{0} < ε

, állításunkat ezzel bebizonyítjuk.
Jelöljük az

f_{i}

g_{j}

egyenesek metszéspontját

Q_{i j}

-ve1, a

Q

csúcsú és

f

g

tengelyű

T

téglalap csúcsait pedig

Q_{i j}'

-vel (

Q_{11} \equiv Q_{11}' \equiv Q

). Az

f_{2}

g_{2}

egyenesek a

Q_{21}'

Q_{12}'

csúcsokból

T

belseje felé indulnak, így metszéspontjuk,

Q_{22}

T

belsejében van. Mivel

Q_{12}

Q_{12}' Q_{22}

szakaszon van,

Q_{12}

T

belsejében van, hasonló módon kapjuk, hogy

Q_{21}

T

belsejében van, tehát a

Q Q_{12} Q_{22} Q_{21}

négyszög

T

belsejében van,

T

pedig az

R_{0}

középpontú,

ε

sugarú kör belsejében, így a

Q Q_{12} / Q_{22} Q_{21}

négyszög pontjainak

R_{0}

-tól mért távolsága kisebb

ε

-nál. ‐
Ezt akartuk bizonyítani.

Prőhle Tamás (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)

dolgozatát felhasználva kiegészítésekkel

II. megoldás. Válasszuk derékszögű koordináta-rendszerünk

x

tengelyének az

e

egyenest és legyenek adott pontjaink koordinátái:

B (0, b)

‐ ahol

b > 0

‐ és

A (d, a)

, továbbá

P (x, 0)

. Így

P A = \sqrt[]{{(x - d)}^{2} + a^{2}}

, és

R

koordinátái:

\begin{matrix} y_{R} = P A \cdot sin B P O ∢ = \frac{b \sqrt[]{{(x - d)}^{2} + a^{2}}}{\sqrt[]{x^{2} + b^{2}}}, \\ x_{R} = x - P A \cdot cos B P O ∢ = x - \frac{x \sqrt[]{{(x - d)}^{2} + a^{2}}}{\sqrt[]{x^{2} + b^{2}}} . \end{matrix}

A koordinátákat megadó két függvénynek a végtelenben vett határértéke ‐ amennyiben mindkettő létezik ‐ megadja a kérdéses határhelyzet megfelelő koordinátáit.
Az átalakítással adódó

\begin{matrix} y_{R} = b \cdot \sqrt[]{\frac{{(1 - \frac{d}{x})}^{2} + {(\frac{a}{x})}^{2}}{1 + {(\frac{b}{x})}^{2}}} \end{matrix}

kifejezésben a

d / x

a / x

b / x

határértéke (a plusz végtelenben és a mínusz végtelenben egyaránt)

0

, így a gyök alatt a számláló és a nevező határértéke egyaránt

1

, hányadosuknak és négyzetgyökének határértéke

1

, ezért

y_{R}

határértéke létezik, és

\begin{matrix} {lim}_{x \to + \infty}^{} y_{R} = b . \end{matrix}

Hasonlóan, a számláló konjugáltjával bővítve, majd a legutóbbihoz hasonló meggondolás-sorozattal

\begin{matrix} x_{R} = \frac{x (\sqrt[]{x^{2} + b^{2}} - \sqrt[]{{(x - d)}^{2} + a^{2}})}{\sqrt[]{x^{2} + b^{2}}} = \frac{x (x^{2} + b^{2} - {(x - d)}^{2} - a^{2})}{\sqrt[]{x^{2} + b^{2}} (\sqrt[]{x^{2} + b^{2}} + \sqrt[]{{(x - d)}^{2} + a^{2}})} = \\ = \frac{2 d x^{2} + (b^{2} - d^{2} - a^{2}) x}{(x^{2} + b^{2}) + \sqrt[]{(x^{2} + b^{2}) {{(x - d)}^{2} + a^{2}}}} = \frac{2 d + \frac{b^{2} - d^{2} - a^{2}}{x}}{1 + {(\frac{b}{x})}^{2} + \sqrt[]{{1 + {(\frac{b}{x})}^{2}} {{(1 - \frac{d}{x})}^{2} + {(\frac{a}{x})}^{2}}}}, \end{matrix}

a nevező határértéke

2

, a számlálóé

2 d

, és így

\begin{matrix} {lim}_{x \to + \infty}^{} x_{R} = d . \end{matrix}

Minthogy mindkét határérték létezik, azért a keresett határhelyzet is létezik, és koordinátái (

d

b

), tehát a határhelyzet az

A

-n át az

y

tengellyel és

B

-n át az

x

tengellyel párhuzamosan húzott egyenesek metszéspontja, az I. megoldásbeli

R_{0}

pont.

Sashegyi László (Tatabánya, Árpád Gimn., III. o. t.)

Bihari Imre (Debrecen, Fazekas M. Gimn., III. o. t.)